Differentiable Programming

Initial Set-Up

# Autograd is maintained but not further developed. However the replacement
# (JAX) is not compatible natively with Windows yet.
import autograd.numpy as np  # Numpy Drop-in Replacement

Predecessor and Successor

def predecessor(a: int) -> int:
    return np.subtract(a, 1)


assert predecessor(1) == 0
assert predecessor(10) == 9

def successor(a: int) -> int:
    return np.add(a, 1)


assert successor(0) == 1
assert successor(10) == 11

Addition

def addition(addend_1: int, addend_2: int) -> int:
    return np.add(addend_1, addend_2)


assert addition(0, 0) == 0
assert addition(1, 0) == 1
assert addition(0, 1) == 1
assert addition(10, 10) == 20

Multiplication

def multiplication(multiplicand: int, multiplier: int) -> int:
    return np.multiply(multiplicand, multiplier)


assert multiplication(0, 0) == 0
assert multiplication(2, 0) == 0
assert multiplication(0, 2) == 0
assert multiplication(10, 10) == 100

Exponentiation

def exponentiation(base: int, exponent: int) -> float:
    return np.power(base, exponent)


assert exponentiation(1, 0) == 1
assert exponentiation(0, 1) == 0
assert exponentiation(3, 3) == 27

What is the particularity of the Differentiable Paradigm?

from autograd import elementwise_grad as egrad
import matplotlib.pyplot as plt
import functools

plt.style.use("bmh")
plt.rcParams["figure.figsize"] = 16, 9

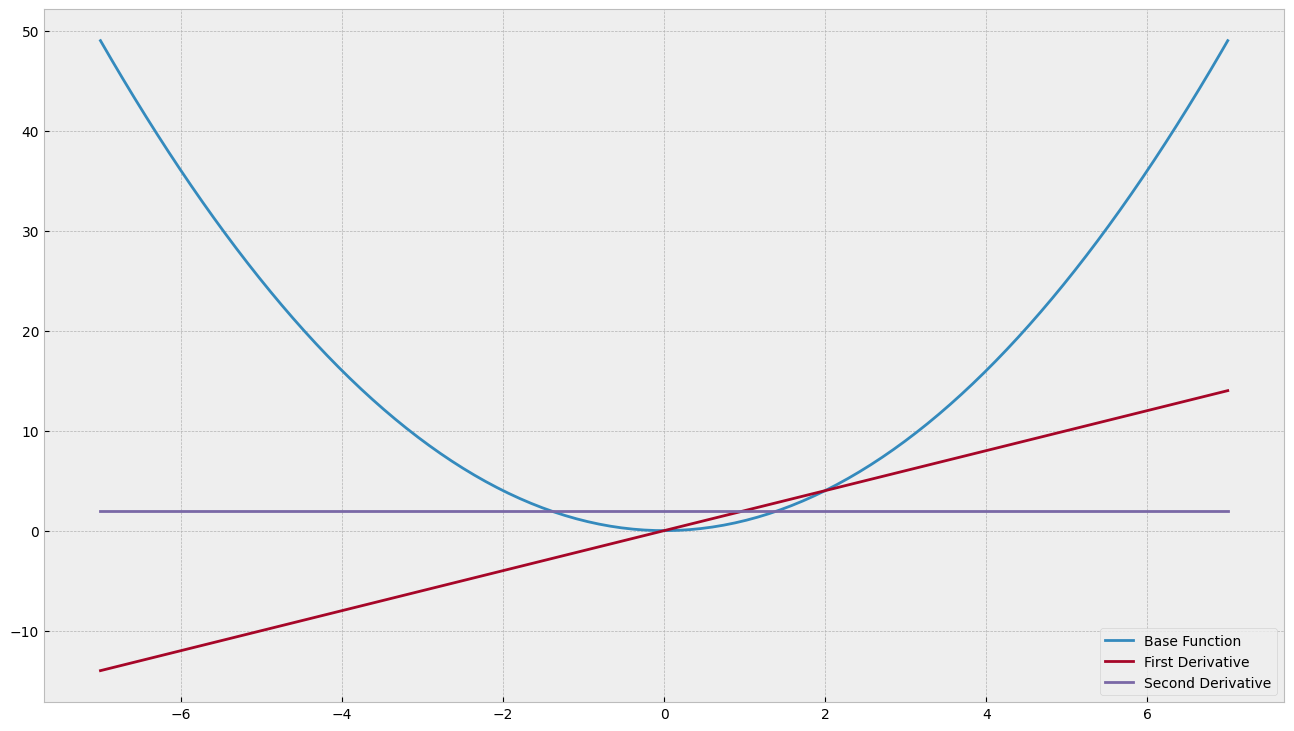
x = np.linspace(-7, 7, 200)
two_power = functools.partial(exponentiation, exponent=2)
plt.plot(x, two_power(x), label="Base Function")
plt.plot(x, egrad(two_power)(x), label="First Derivative")
plt.plot(x, egrad(egrad(two_power))(x), label="Second Derivative")
plt.legend()
plt.show()