1. Introducción a la Teoría de Control Con Matlab#

Version 0.1

Contenido Original creado por Ezequiel Leonardo Castaño

Este contenido está en BORRADOR y puede estar incompleto y/o sufrir modificaciones

Enlaces Útiles:

Los demás capítulos pueden encontrarse en el homepage.
El repositorio completo está disponible en Github como Control Theory With Matlab
Ante dudas y sugerencias, no dudes en utilizar los Github Issues

%plot inline --format=png -w 1600

format compact;

1.1. Transformada de Laplace#

1.1.1. Definición#

La transformada de Laplace es una generalización de la transformada de Fourier

La transformada de Fourier convierte una función del dominio del tiempo al dominio de la frecuencia

\[X(\omega )=\int_{-\infty }^{\infty } x(t)e^{-j\omega t} dt\]

El término \(e^{-j\omega t}\) es la forma exponencial de una función senoidal, donde \(j\) representa a la unidad imaginaria. Sin embargo, esta transformación resulta bastante restrictiva ya que no hay componentes exponenciales puras.

Para añadir un componente exponencial, se agrega un factor exponencial a la función \(x(t)\)quedando:

\[X(\sigma ,\omega )=\int_{-\infty }^{\infty } [x(t)\cdot e^{-\sigma t} ]e^{-j\omega t} dt\]

1.1.2. Desarrollo#

Al trabajar algebraicamente se tiene

\[X(\sigma ,\omega )=\int_{-\infty }^{\infty } x(t)\cdot [e^{-\sigma t} \cdot e^{-j\omega t} ]dt\]

\[X(\sigma ,\omega )=\int_{-\infty }^{\infty } x(t)\cdot e^{-\sigma t-j\omega t} dt\]

\[X(\sigma ,\omega )=\int_{-\infty }^{\infty } x(t)\cdot e^{-(\sigma -j\omega )t} dt\]

Y luego se reemplaza a la expresión \(\sigma -j\omega\) por una nueva variable compleja llamada \(s\), donde \(\sigma\) es la parte real y \(\omega\) la parte imaginaria, este nuevo dominio diferente del tiempo se conoce como plano \(s\).

\[X(s)=\int_{-\infty }^{\infty } x(t)e^{-st} dt\]

Esta forma de expresar a la función \(x(t)\) como \(X(s)\)es lo que se conoce como transformada de Laplace, símbolicamente se representa

\[\mathcal{L}\lbrace x(t)\rbrace =X(s)\]

Análogamente para la transformación inversa

\[{\mathcal{L}}^{-1} \lbrace X(s)\rbrace =x(t)\]

1.2. Propiedades#

Algunas de las propiedades de la transformada de Laplace son

1.2.1. Linearidad#

\[\mathcal{L}\lbrace a\cdot f(t)+b\cdot g(t)\rbrace =a\cdot F(s)+b\cdot G(s)\]

1.2.2. Retraso o Delay#

Dada una función escalón definida por \(\gamma (t-a)=\left\lbrace \begin{array}{lcc} 0 & si & x\le a\\ 1 & si & x\ge a \end{array}\right.\)

\[\mathcal{L}\lbrace f(t-a)\cdot \gamma (t-a)\rbrace =e^{-as} \cdot F(s)\]

1.2.3. Derivada#

\[\mathcal{L}\lbrace f^{^{\prime } } (t)\rbrace =s\cdot F(s)-f(0)\]

\[\mathcal{L}\lbrace f^{^{\prime \prime } } (t)\rbrace =s^2 \cdot F(s)-s\cdot f(0)-f^{^{\prime } } (0)\]

1.2.4. Integral#

\[\mathcal{L}\lbrace \int_0^t f(t)dt\rbrace =\frac{1}{s}\mathcal{L}\lbrace f(t)\rbrace\]

1.2.5. Teorema del valor inicial#

\[\lim_{s\to \infty } (s\cdot F(s))=\lim_{t\to 0} f(t)\]

1.2.6. Teorema del valor final}#

\[\lim_{s\to 0} (s\cdot F(s))=\lim_{t\to \infty } f(t)\]

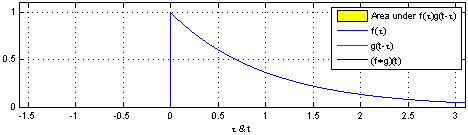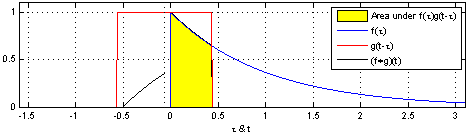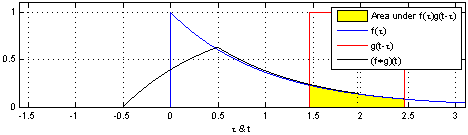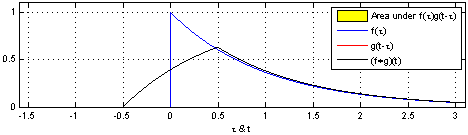
1.2.7. Convolución#

\[\mathcal{L}\lbrace f(t)*g(t)\rbrace =F(s)\cdot G(s)\]

La operación convolución puede verse gráficamente en esta animación (Fuente)

1.3. Transformaciones comunes#

Normalemente en lugar de hacer la integral, que puede llevar mucho tiempo, se recurre a tablas que tienen las transformadas pre-calculadas. Algunas de las transformadas más comunes son:

1.3.1. Función impulso#

\[\mathcal{L}\lbrace \delta (c)\rbrace =c\]

1.3.2. Función escalón#

\[\mathcal{L}\lbrace c\rbrace =\frac{c}{s}\]

1.3.3. Función rampa#

\[\mathcal{L}\lbrace c\cdot t\rbrace =\frac{c}{s^2 }\]

1.3.4. Función exponencial#

\[\mathcal{L}\lbrace e^{a\cdot t} \rbrace =\frac{1}{s-a}\]

1.4. Laplace en Matlab#

Definimos los símbolos a utilizar

a = sym("a");
t = sym("t", 'positive');
s = sym("s");

A continuación se muestran algunos ejemplos con sus transformadas y antitransformadas

1.4.1. Escalón#

funcion = a;
transformada = laplace(funcion, t, s)

transformada =
a/s

transformada_inversa = ilaplace(transformada)

transformada_inversa =
a

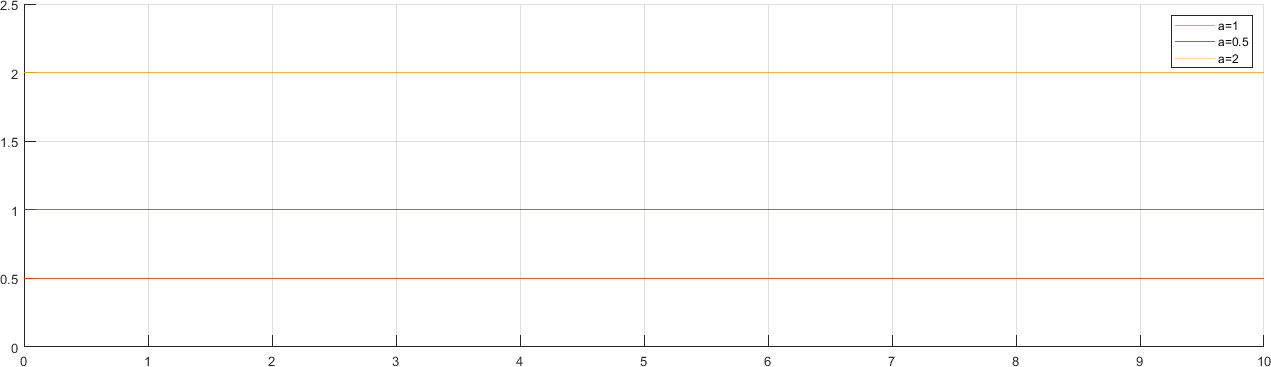
1.4.1.1. Ejemplo Gráfico#

syms f(t) g(t) h(t);
f(t) = 1;
g(t) = 0.5;
h(t) = 2;

figure;
hold on;
fplot([f, g, h], [0 10])
ylim([0 2.5])
grid on
legend("a=1", "a=0.5", "a=2")

../_images/ELC01_Transformada_de_Laplace_18_1.png

1.4.2. Rampa#

funcion = a * t;
transformada = laplace(funcion, t, s)

transformada =
a/s^2

transformada_inversa = ilaplace(transformada)

transformada_inversa =
a*t

1.4.2.1. Ejemplo Gráfico#

syms f(t) g(t) h(t);
f(t) = 1 * t;
g(t) = 0.5 * t;
h(t) = 2 * t;

figure;
hold on;
fplot([f, g, h], [0 10])
ylim([0 10])
grid on
legend("a=1", "a=0.5", "a=2")

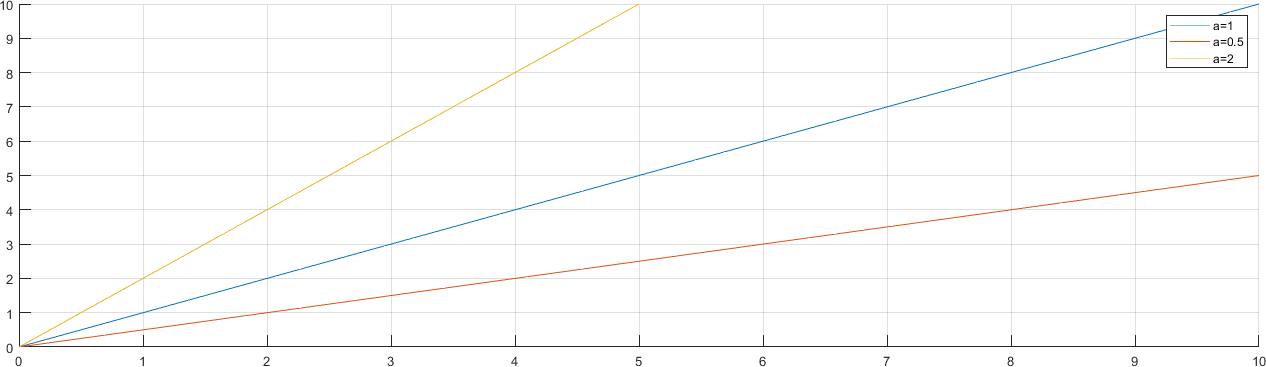
../_images/ELC01_Transformada_de_Laplace_23_1.png

1.4.3. Exponencial#

funcion = exp(-a*t);
transformada = laplace(funcion, t, s)

transformada =
1/(a + s)

transformada_inversa = ilaplace(transformada)

transformada_inversa =
exp(-a*t)

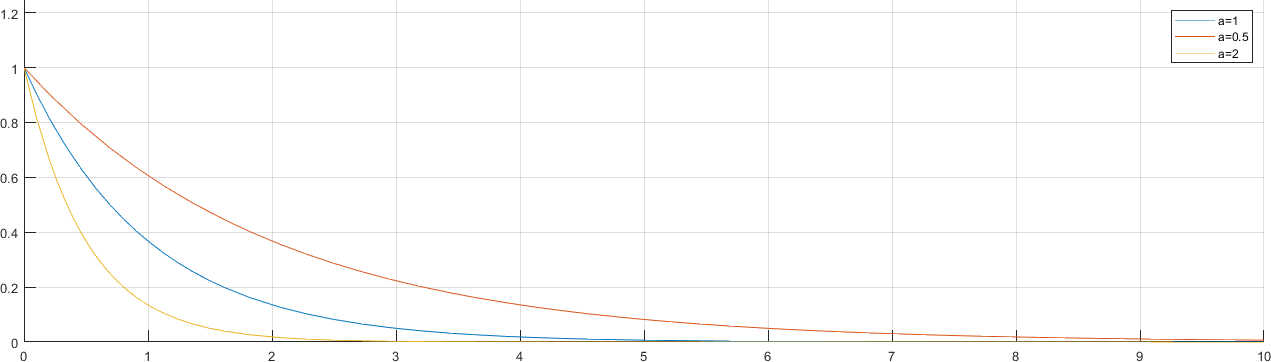
1.4.3.1. Ejemplo Gráfico#

syms f(t) g(t) h(t);
f(t) = exp(-1 * t);
g(t) = exp(-0.5 * t);
h(t) = exp(-2 * t);

figure;
hold on;
fplot([f, g, h], [0 10])
ylim([0 1.25])
grid on
legend("a=1", "a=0.5", "a=2")

../_images/ELC01_Transformada_de_Laplace_28_1.png

1.4.4. Derivada#

syms f(t);
derivada = diff(f, t);
transformada = laplace(derivada, t, s)

transformada =
s*laplace(f(t), t, s) - 1*f(0)

transformada_inversa = ilaplace(transformada)

transformada_inversa =
diff(f(t), t)

integral = int(f, t, 0, t);
transformada = laplace(integral, t, s)

transformada =
laplace(int(f(t), t, 0, t), t, s)

transformada_inversa = ilaplace(transformada)

transformada_inversa =
int(f(t), t, 0, t)

1.5. Ejercicios#

s = sym("s");

1.5.1. Estructura General de un ejercicio#

Se define una función cuya antitransformada se desea calcular

funcion_transformada = 12 / ((s-3)*(s+1))

funcion_transformada =
12/((s + 1)*(s - 3))

Se utiliza la función partfrac para separar en fracciones parciales

fracciones_parciales = partfrac(funcion_transformada)

fracciones_parciales =
3/(s - 3) - 3/(s + 1)

Se calcula la antitransformada a las fracciones parciales

ilaplace(fracciones_parciales)

ans =
3*exp(3*t) - 3*exp(-t)

Se verifica haciendo la antitransformada de la función original

ilaplace(funcion_transformada)

ans =
3*exp(3*t) - 3*exp(-t)

1.5.2. Ejercicios Adicionales#

Ejercicio 1

funcion_transformada = (4) / (s^2 - 9)

funcion_transformada =
4/(s^2 - 9)

fracciones_parciales = partfrac(funcion_transformada)

fracciones_parciales =
0.6667/(s - 3) - 0.6667/(s + 3)

ilaplace(fracciones_parciales)

ans =
0.6667*exp(3*t) - 0.6667*exp(-3*t)

Ejercicio 2

funcion_transformada = (s^2+2*s+3) / (s+1)^2

funcion_transformada =
(s^2 + 2*s + 3)/(s + 1)^2

fracciones_parciales = partfrac(funcion_transformada)

fracciones_parciales =
2/(s + 1)^2 + 1

ilaplace(fracciones_parciales)

ans =
2*t*exp(-t)

Ejercicio 3

funcion_transformada = (5*(s+2)) / (s^2*(s+1)*(s+3))

funcion_transformada =
(5*s + 10)/(s^2*(s + 1)*(s + 3))

fracciones_parciales = partfrac(funcion_transformada)

fracciones_parciales =
2.5000/(s + 1) + 0.2778/(s + 3) - 2.7778/s + 3.3333/s^2

ilaplace(fracciones_parciales)

ans =
3.3333*t + 2.5000*exp(-t) + 0.2778*exp(-3*t) - 2.7778

Teoría de Control con Matlab

Introducción a la Teoría de Control Con Matlab

Chapter Index