Sintonización
Chapter Index
7. Sintonización#
Version 0.1
Contenido Original creado por Ezequiel Leonardo Castaño
Este contenido está en BORRADOR y puede estar incompleto y/o sufrir modificaciones
%plot inline --format=png -w 1600 -h 500
format compact;
7.1. Sintonización#
El proceso de sintonización consiste en modificar las ganancias de un controlador para lograr un comportamiento que se ajuste a los requerimientos de diseño. Existen varias técnicas para la sintonización, el proceso puede verse en la siguiente animación. Fuente
7.2. Sintonización por Curva de Reacción del Proceso (CPR)#
Se remueve el controlador y se evalua la salida en lazo abierto ante una entrada escalón
Sólo se puede aplicar si la salida tiene forma de S
num = [1 3];
den = [1 5 9 5];
sistema = tf(num, den);
lazo_cerrado = feedback(sistema, 1);
[respuesta, tiempo] = step(sistema);
figure;
hold on;
plot(tiempo, respuesta)
yline(1, "--k")
yline(max(respuesta), ":k")
ylim([0 1.1])
xlim([0 3])
grid on
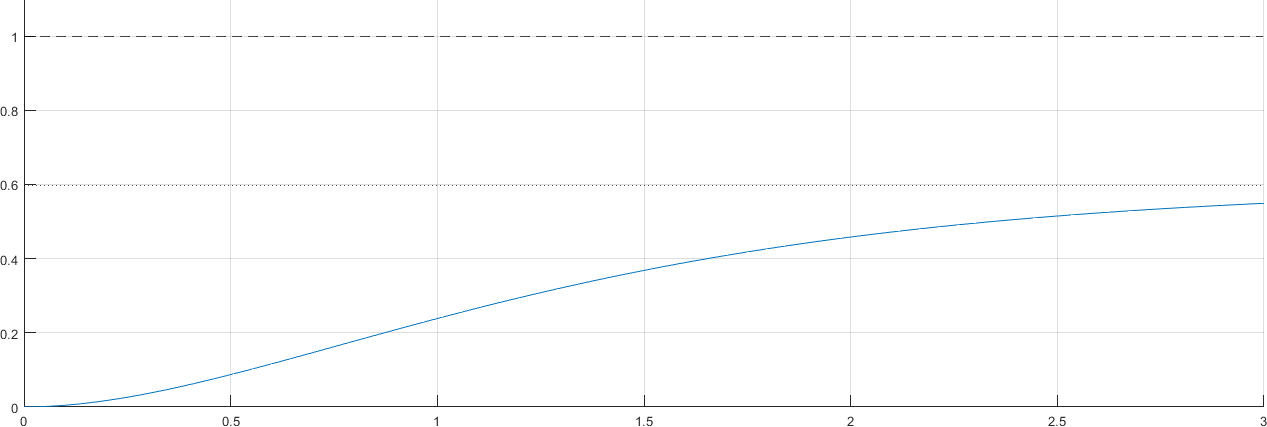
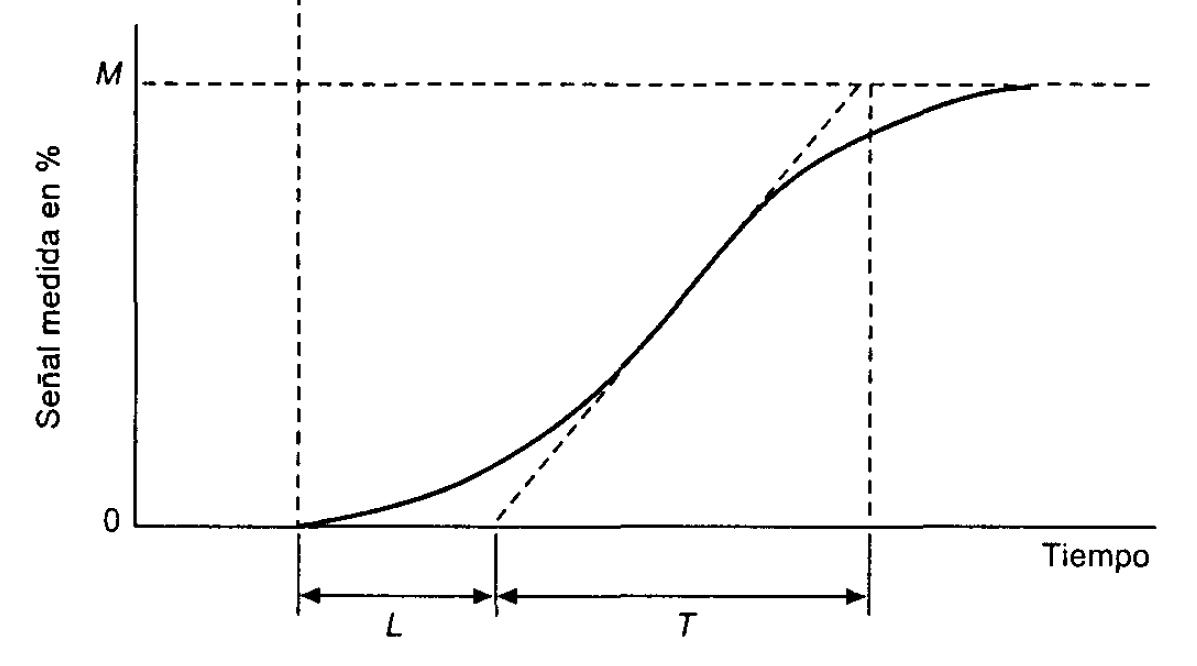
Se calcula en punto de inflexión numéricamente
figure;
hold on
pendiente_en_tiempo = gradient(respuesta, tiempo);
[pendiente, indice_critico] = max(pendiente_en_tiempo);
tiempo_inflexion = tiempo(indice_critico);
respuesta_critica = respuesta(indice_critico);
recta_tangente = pendiente * (tiempo - tiempo_inflexion) + respuesta_critica;
plot(tiempo, respuesta)
plot(tiempo, recta_tangente)
xlim([0 3])
yline(max(respuesta), ":k")
yline(1, "--k")
ylim([0 1.1])
grid on
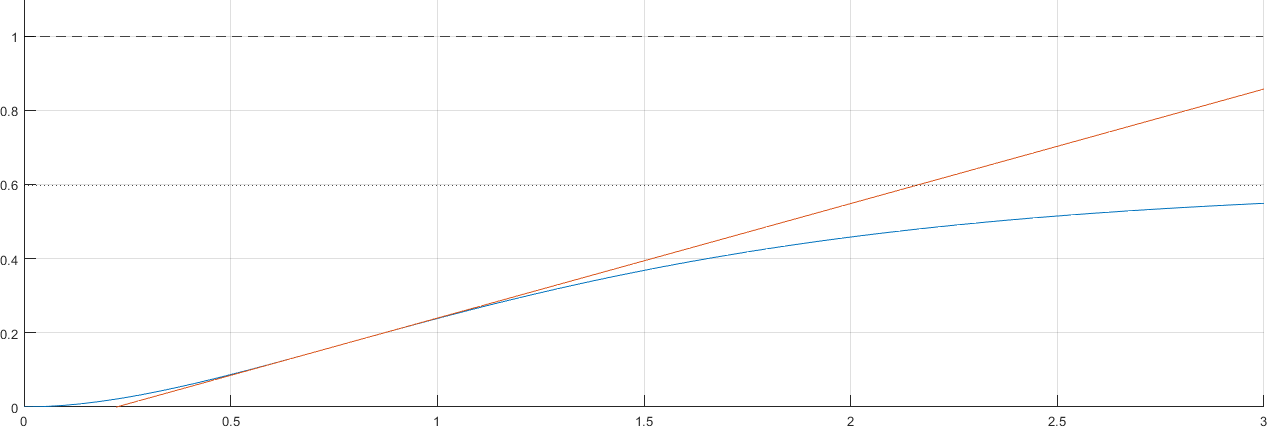
L = tiempo_inflexion - (respuesta_critica/pendiente)
L =
0.2236
Tau = respuesta(end) / pendiente
Tau =
1.9375


7.3. Definiendo controlador Proporcional (P)#
Kp = Tau / L;
controlador_p = tf([Kp], [1]);
lazo_cerrado_p = feedback(controlador_p*sistema, 1);
7.4. Definiendo controlador Proporcional Integral (PI)#
Forma estandar
Kp = 0.9 * Tau / L;
tau_i = L / 0.3;
Forma basada en ganacias
Ki = Kp / tau_i;
controlador_pi = tf([Kp Ki], [1 0]);
lazo_cerrado_pi = feedback(controlador_pi*sistema, 1);
7.5. Definiendo controlador Proporcional Integral Derivativo (PID)#
Usando la forma estandar
Kp = 1.2 * Tau / L;
tau_i = 2 * L;
tau_d = 0.5 * L;
Usando la forma de ganancia
Kp = Kp;
Ki = Kp / tau_i;
Kd = Kp * tau_d;
Definimos controlador PID
controlador_pid = tf([Kd Kp Ki], [1 0]);
lazo_cerrado_pid = feedback(controlador_pid*sistema, 1);
7.6. Comparación de Controladores#
7.6.1. Comparación de Respuesta#
figure;
step(lazo_cerrado, lazo_cerrado_p, lazo_cerrado_pi, lazo_cerrado_pid)
xlim([0 7])
legend("Sin Sintonizar", "P Sintonizado con CRP", "PI Sintonizado con CRP", "PID Sintonizado con CRP")
grid on
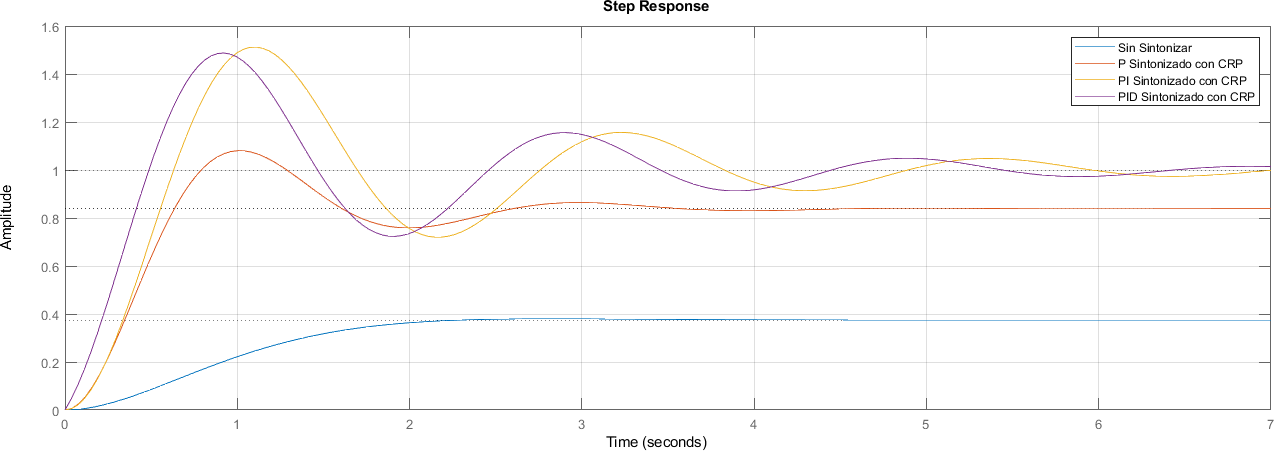
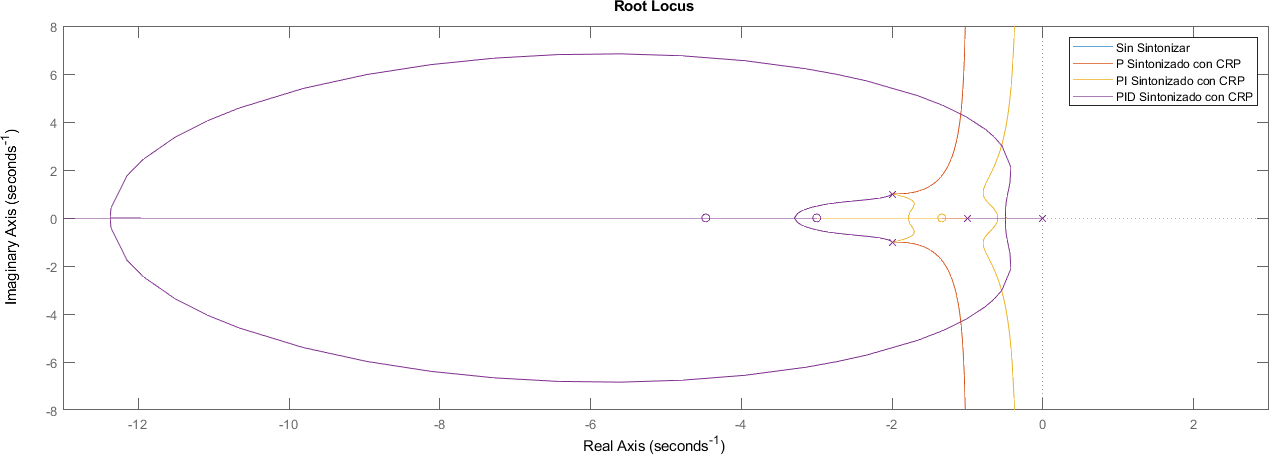
7.6.2. Comparación de ceros y polos#
figure;
rlocus(sistema, controlador_p*sistema, controlador_pi*sistema, controlador_pid*sistema)
legend("Sin Sintonizar", "P Sintonizado con CRP", "PI Sintonizado con CRP", "PID Sintonizado con CRP")
xlim([-13 3])
ylim([-8 8])
7.7. Sintonización por última ganancia o ganancia crítica (GC)#
Es necesario que el lugar geométrico de las raices cruce al eje imaginario para poder aplicar este método
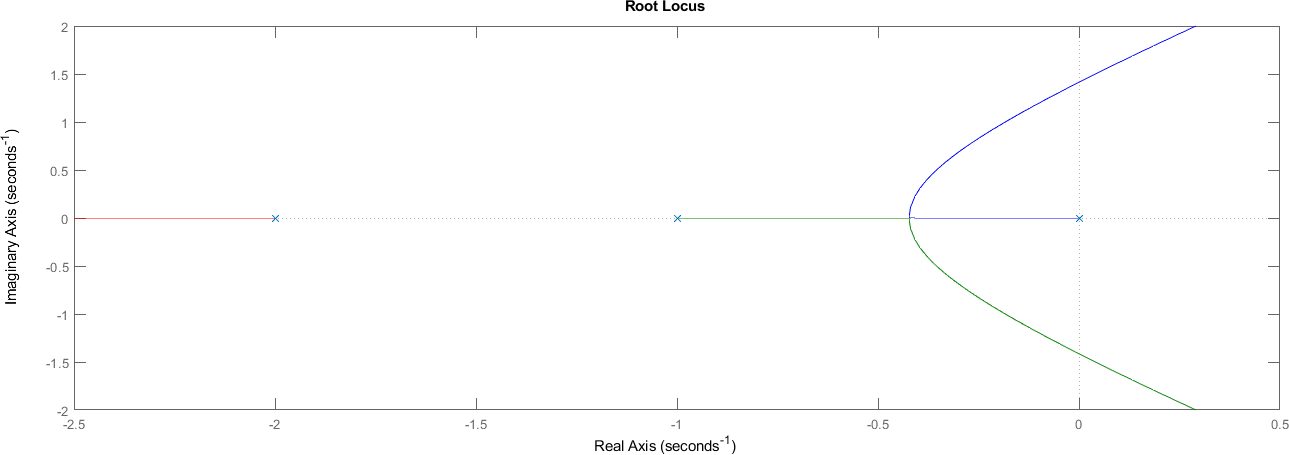
7.8. Verificar Cruce con el eje imaginario#
sistema = tf([1], [1 3 2 0]);
figure;
rlocus(sistema)
xlim([-2.5 0.5])
ylim([-2 2])
7.9. Hallar valor de ganancia crítica \(K\)#
Como las ramas cruzan el eje imaginario, se puede hallar el valor crítico de K. Este valor crítico se puede encontrar con Routh o utilizando el reemplazo de \(s\) con \(j\omega\)
s = sym("s");
K = sym("k", "real");
w = sym("omega", "real");
sistema = K*(s+2) / (s^4 + 7*s^3 + 17.25*s^2 + 5.5*s - 30.75);
lazo_cerrado = sistema / (1 + sistema);
[num, ecuacion_caracteristica] = numden(lazo_cerrado);
remplazar_s = subs(ecuacion_caracteristica, s, j*w);
omega = solve(imag(remplazar_s) == 0, w)
Warning: Solutions are only valid under certain conditions. To include parameters and conditions in the solution, specify the 'ReturnConditions' value as 'true'.
> In sym/solve>warnIfParams (line 478)
In sym/solve (line 357)
omega =
0
-0.2673*(2*k + 11)^(1/2)
0.2673*(2*k + 11)^(1/2)
K_critico = 6
K_critico =
6
Se puede ver como el valor crítico de \(K\) en este sistema es \(6\)
7.10. Hallar el periodo crítico#
El periodo crítico puede hallarse con la expresión \(\frac{2\pi }{\omega }\)
periodo_critico = 2 * pi / sqrt(2); % Obtenido de la variable omega
7.11. Definiendo Controladores#
sistema = tf([1], [1 3 2 0]);
lazo_cerrado = feedback(sistema, 1);

7.12. Definiendo controlador Proporcional (P)#
Kp = 0.5 * K_critico;
controlador_p = tf([Kp], [1]);
lazo_cerrado_p = feedback(controlador_p*sistema, 1);
7.13. Definiendo controlador Proporcional Integral (PI)#
Forma estandar
Kp = 0.45 * K_critico;
tau_i = 1/1.2 * periodo_critico;
Forma basada en ganacias
Ki = Kp / tau_i;
controlador_pi = tf([Kp Ki], [1 0]);
lazo_cerrado_pi = feedback(controlador_pi*sistema, 1);
7.14. Definiendo controlador Proporcional Integral Derivativo (PID)#
Usando la forma estandar
Kp = 0.6 * K_critico;
tau_i = 0.5 * periodo_critico;
tau_d = 0.125 * periodo_critico;
Usando la forma de ganancia
Kp = Kp;
Ki = Kp / tau_i;
Kd = Kp * tau_d;
Definimos controlador PID
controlador_pid = tf([Kd Kp Ki], [1 0]);
lazo_cerrado_pid = feedback(controlador_pid*sistema, 1);
7.15. Comparación de Controladores#
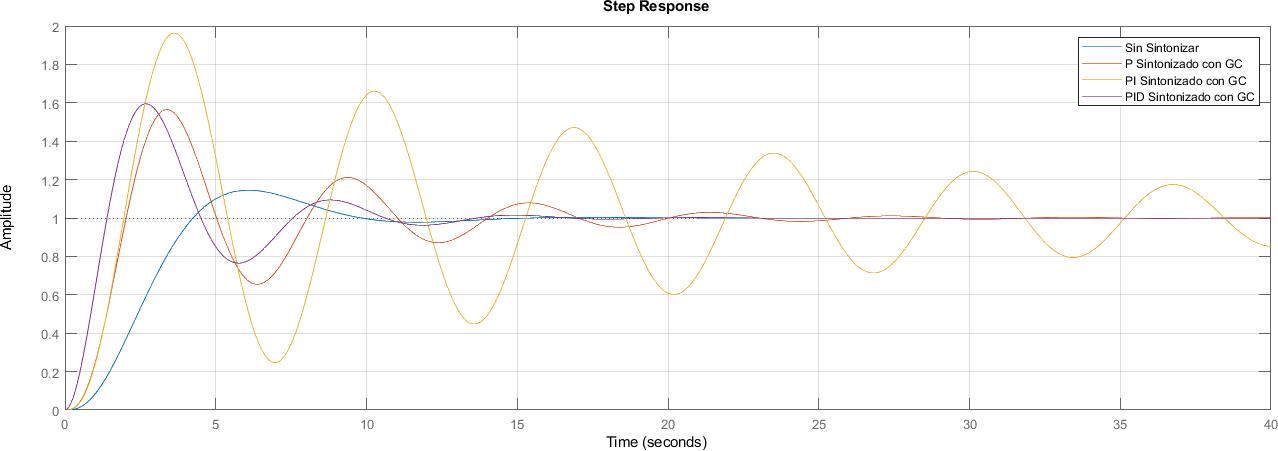
7.15.1. Comparación de Respuesta#
figure;
step(lazo_cerrado, lazo_cerrado_p, lazo_cerrado_pi, lazo_cerrado_pid)
legend("Sin Sintonizar", "P Sintonizado con GC", "PI Sintonizado con GC", "PID Sintonizado con GC")
xlim([0 40])
grid on
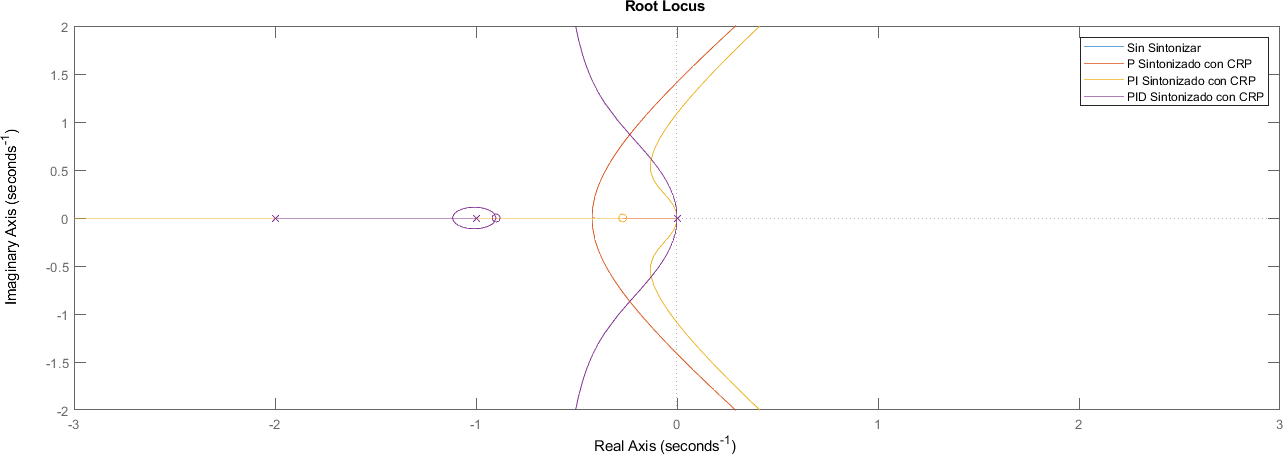
7.15.2. Comparación de ceros y polos#
figure;
rlocus(sistema, controlador_p*sistema, controlador_pi*sistema, controlador_pid*sistema)
legend("Sin Sintonizar", "P Sintonizado con CRP", "PI Sintonizado con CRP", "PID Sintonizado con CRP")
xlim([-3 3])
ylim([-2 2])
7.16. Sintonización por fuerza Bruta#
Sintonizar el sistema para que cumpla con los siguientes requisitos ante una entrada escalón
Tiempo de Asentamiento al 2% a los 10s
Error de estado estacionario nulo
Overshoot de menos del 20%
La función de transferencia de la planta es
Tener en cuenta las siguientes consideraciones
Se asume sensor ideal (retroalimentación unitaria)
El valor máximo de la ganancia proporcional es de 5
El valor máximo de la ganancia integral es de 5
El valor máximo de la ganancia derivativa es de 2
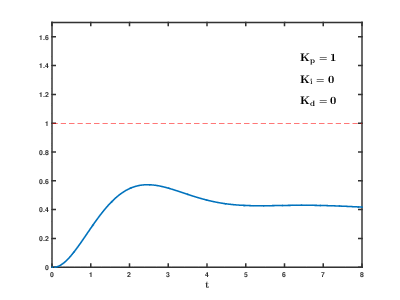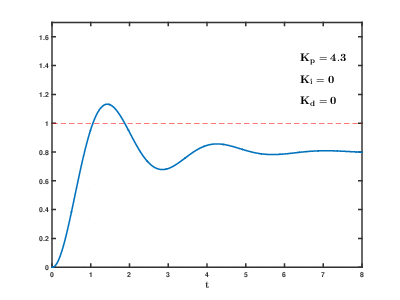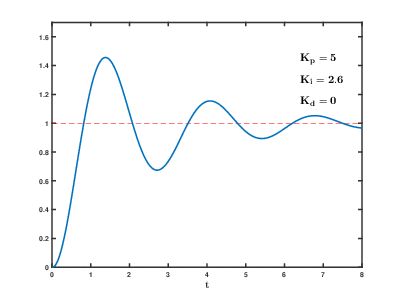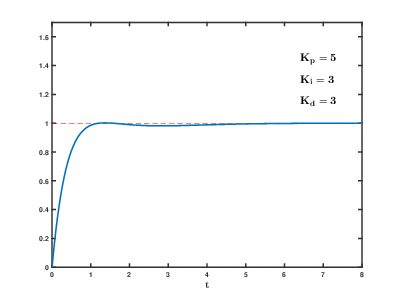
7.17. 1. Hallando Ganancia Proporcional \(K_p\)#
s = tf("s");
Kd = 0;
Ki = 0;
kps = [1 2 3 4 5];
ceros = transpose([-2]);
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
for index = 1:length(kps)
Kp = kps(index);
controlador = Kp + Ki / s + Kd * s;
lazo_cerrado_{index} = feedback(sistema*controlador, 1);
legend_info{index} = ['Kp = ' num2str(Kp)];
end
figure;
hold on
step(lazo_cerrado_{:})
title("Salida en lazo cerrado")
xlim([0 40])
ylim([0 1.15])
yline(1, "--k")
legend(legend_info)
grid on
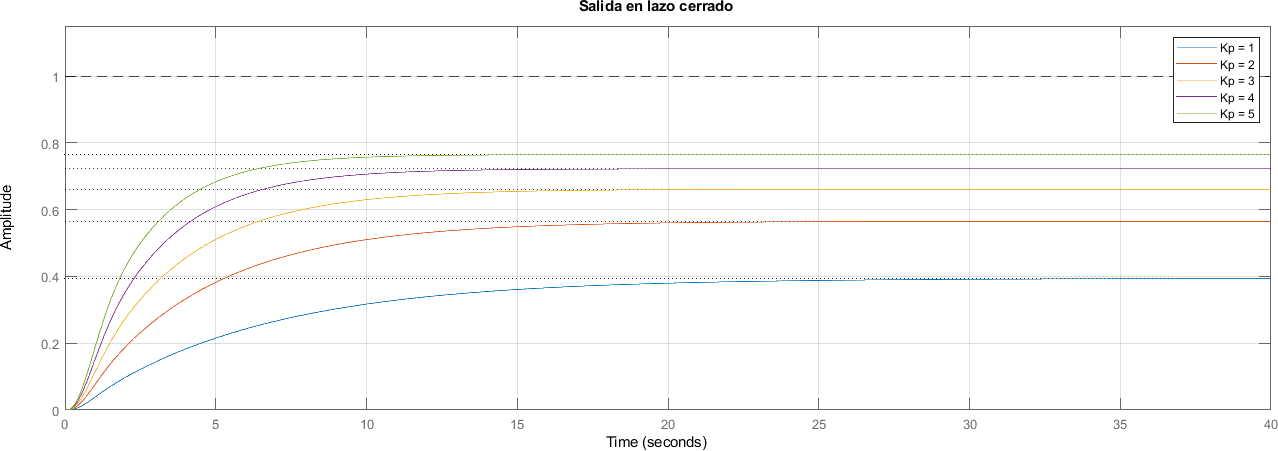
7.18. 2. Hallando Ganancia Integral \(K_i\)#
s = tf("s");
Kp = 5;
Kd = 0;
kis = 0:0.05:1;
ceros = transpose([-2]);
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
for index = 1:length(kis)
Ki = kis(index);
controlador = Kp + Ki / s + Kd * s;
lazo_cerrado_{index} = feedback(sistema*controlador, 1);
legend_info{index} = ['Ki = ' num2str(Ki)];
end
figure;
hold on
step(lazo_cerrado_{:})
xlim([0 40])
title("Salida en lazo cerrado")
legend(legend_info)
grid on
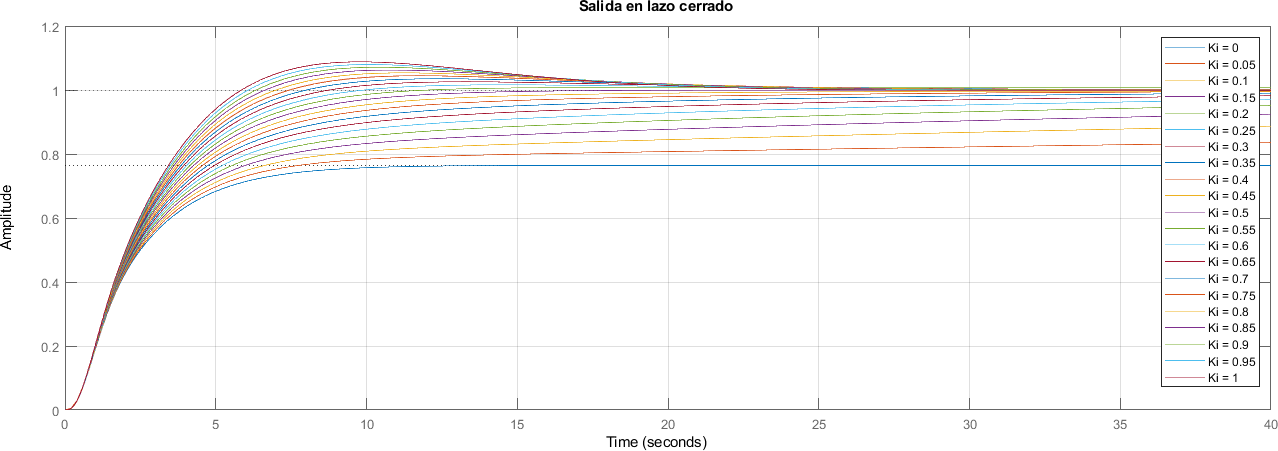
7.19. 3. Hallando Ganancia Derivativa \(K_d\)#
s = tf("s");
Kp = 5;
Ki = 0.5;
kds = 0:0.1:0.5;
ceros = transpose([-2]);
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
for index = 1:length(kds)
Kd = kds(index);
controlador = Kp + Ki / s + Kd * s;
lazo_cerrado_{index} = feedback(sistema*controlador, 1);
legend_info{index} = ['Kd = ' num2str(Kd)];
end
figure;
hold on
step(lazo_cerrado_{:})
xlim([0 40])
title("Salida en lazo cerrado")
legend(legend_info)
grid on
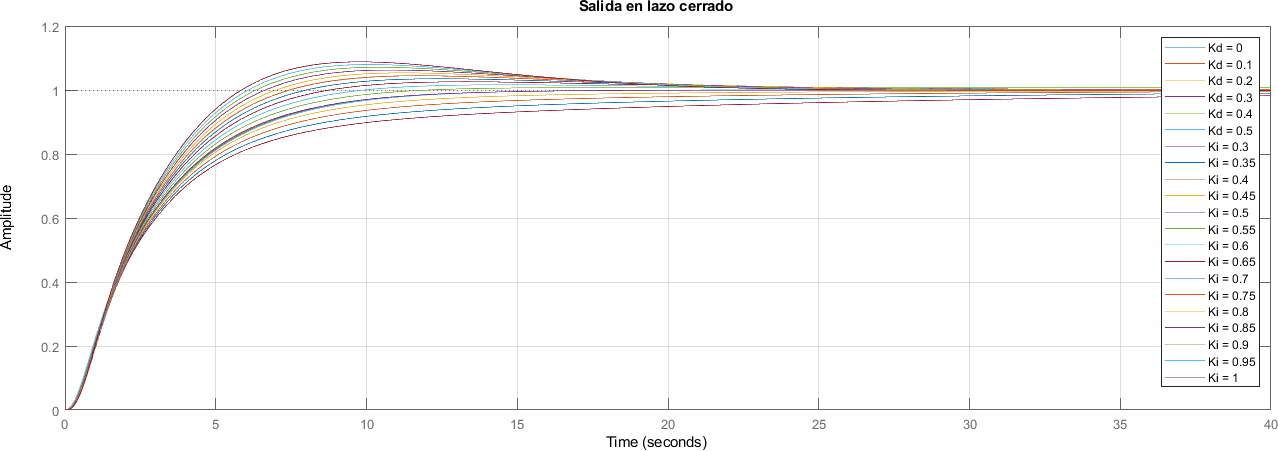
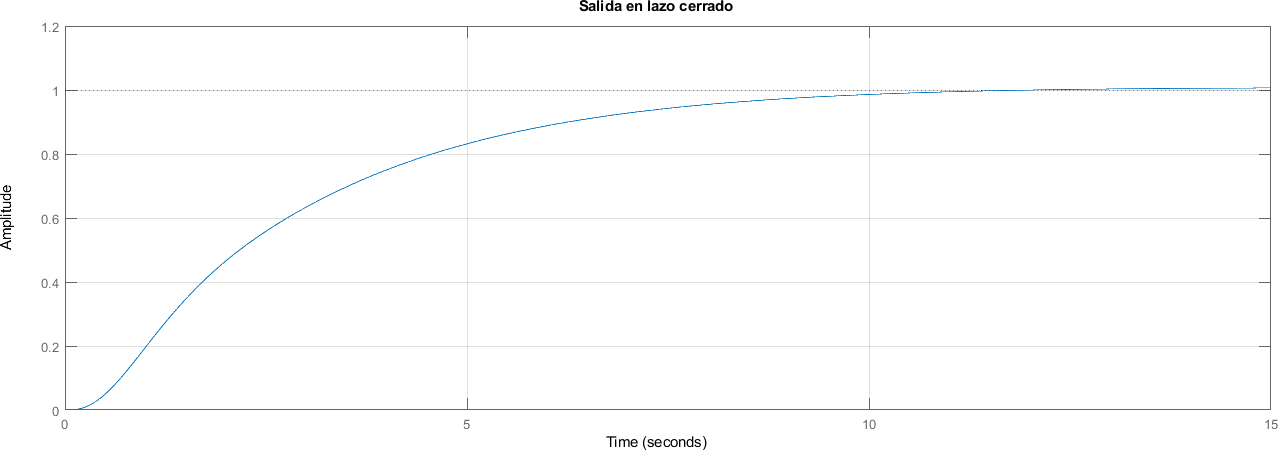
7.20. Sistema Sintonizado#
s = tf("s");
Kp = 5;
Ki = 0.55;
Kd = 0;
ceros = transpose([-2]);
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
controlador = Kp + Ki / s + Kd * s;
lazo_cerrado = feedback(sistema*controlador, 1);
figure;
hold on
step(lazo_cerrado)
title("Salida en lazo cerrado")
grid on
7.21. Sintonización Automática con Simulink#
Para poder utilizar la sintonización automática con Simulink hace falta seguir los siguientes pasos:
7.22. 1. Declarar las ganancias en el Workspace de Matlab#
Kp = 1;
Ki = 1;
Kd = 1;
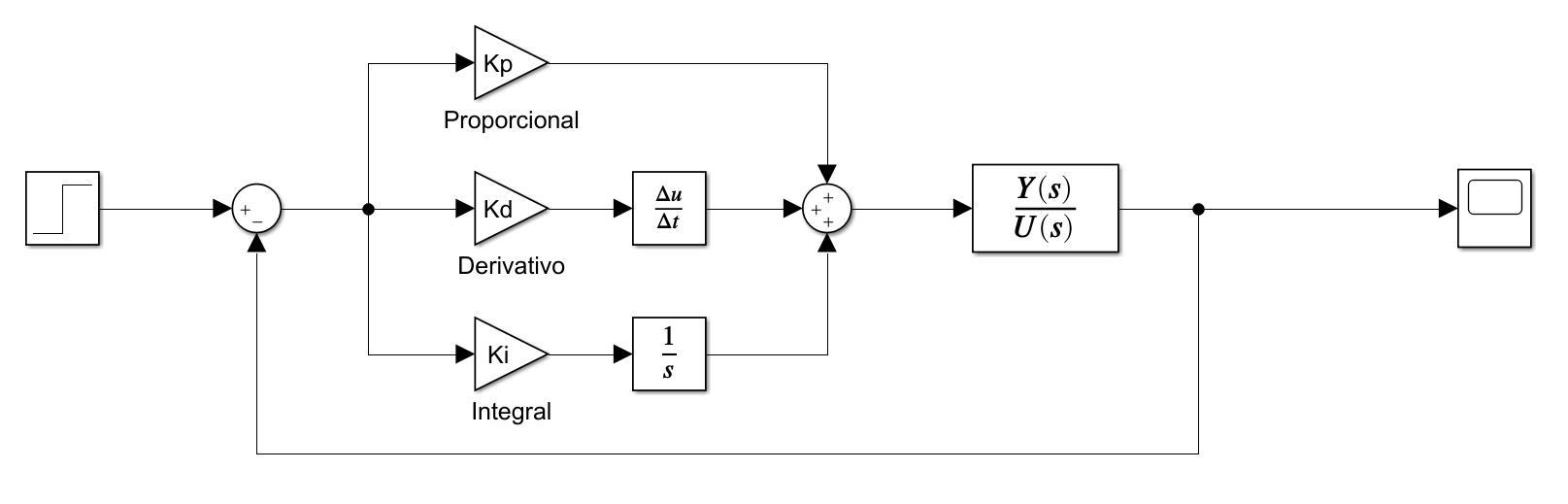
7.23. 2. Construir un modelo en Simulink utilizando un controlador PID con los bloques básicos#
Aclaraciónes importantes:
No utilizar el bloque PID que viene por defecto con Simulink porque no es compatible con la herramienta que se utilizará después
Los valores de las ganancias tienen que ser los mismos nombres de las variables definidos previamente en matlab
La función de transferencia tiene que definirse utilizando numerador y denominador. Si sólo se tienen los ceros y polos, usar la función
zp2tfcomo se muestra acontinuación
ceros = [-2];
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
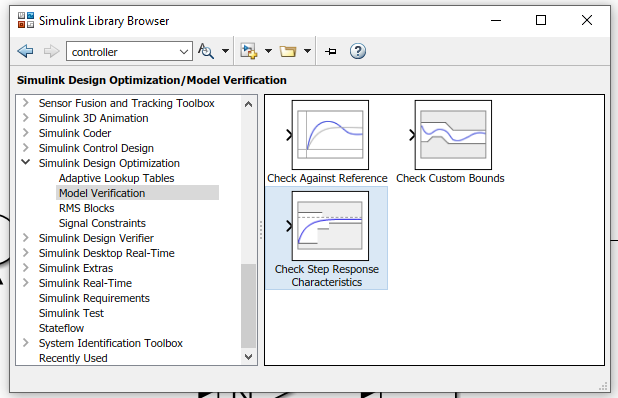
7.24. 3. Agregar Verificación de Características#
Conectar el bloque Check Step Response Characteristics que está dentro de Simulink Design Optimization -> Model Verification y agregarlo a la salida del sistema
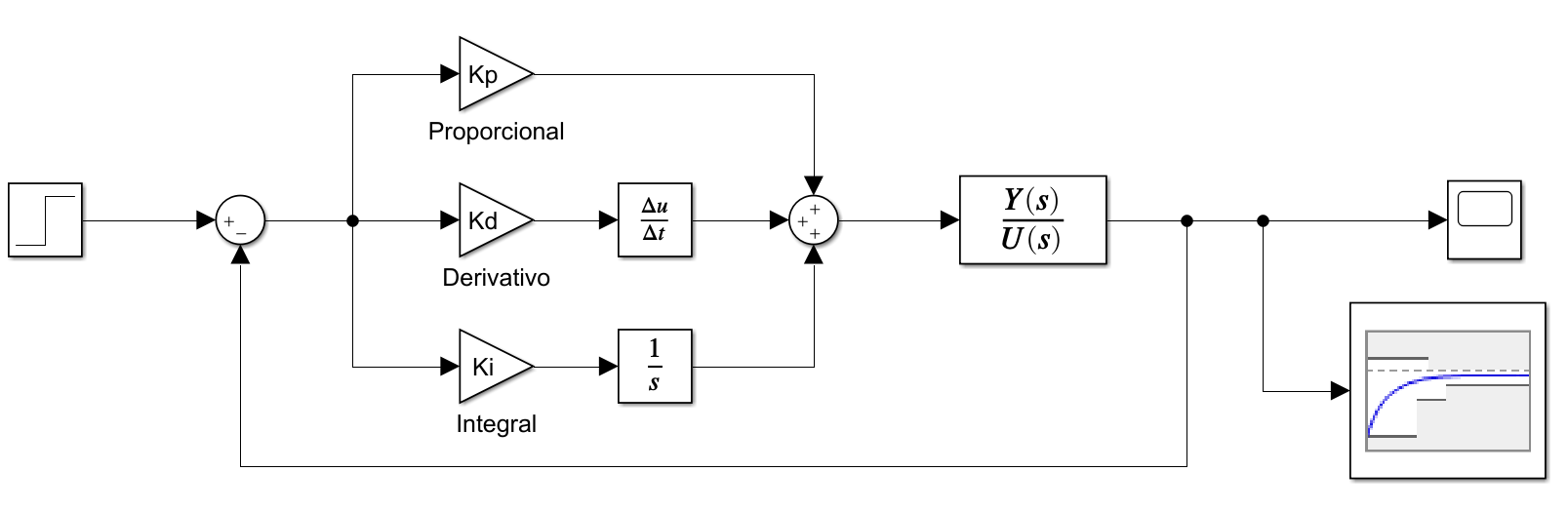
7.25. 4. Abrir el bloque y configurar los requisitos del sistema y presionar Apply#
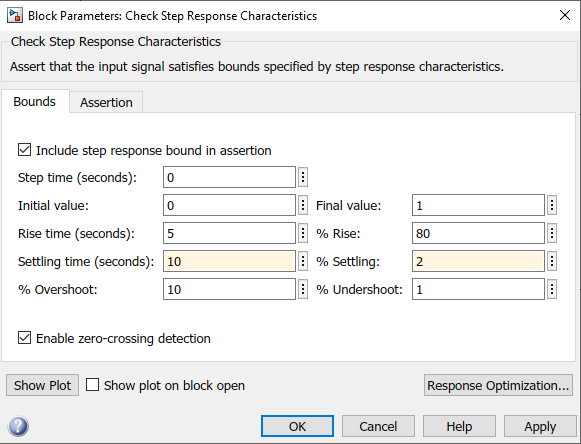
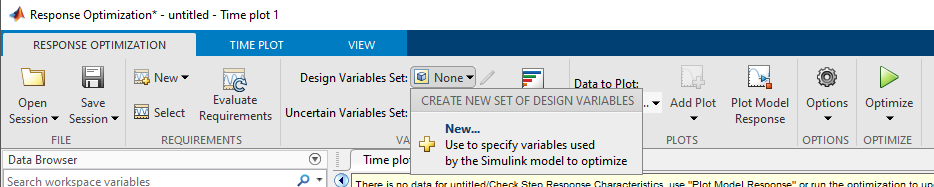
7.26. 5. Presionar el botón Response Optimization y agregar nuevas variables de diseño#
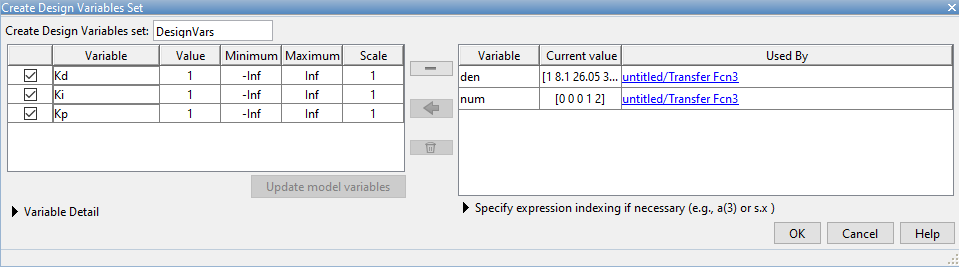
Seleccionar las tres ganancias en la lista de la derecha y pasarlas a la de la izquiera con el botón de la flecha y presionar OK
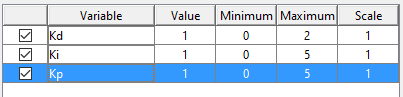
Asegurarse que los límites de las ganancias sean correctos, en este caso el enunciado especificaba límites máximos, pero las ganancias no deberían ser nunca negativas, así que el valor minimo debería ser 0.
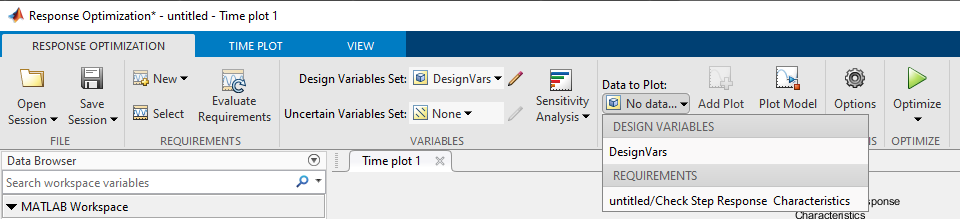
7.27. 6. Elegir el conjunto de variables de diseño y agregar el gráfico de evolución histórica#
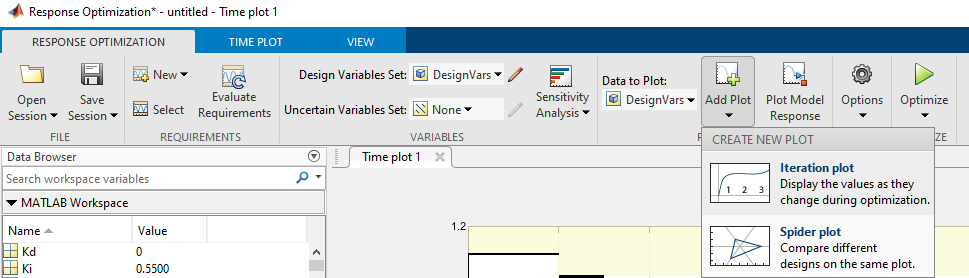
7.28. 7. Ejecutar la simulación y validar que no se cumplen los requisitos de diseño#

Los requisitos se cumplen si toda la gráfica azul está dentro de la zona blanca
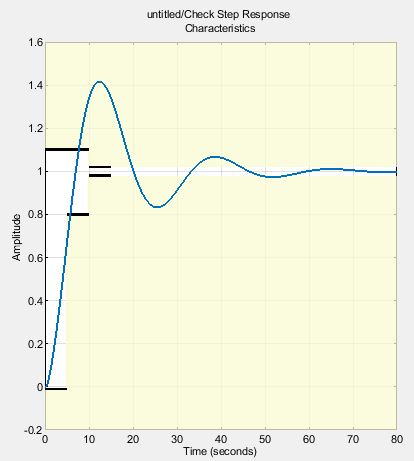
7.29. 8. Acomodar las ventanas de los gráficos y presionar Optimize#
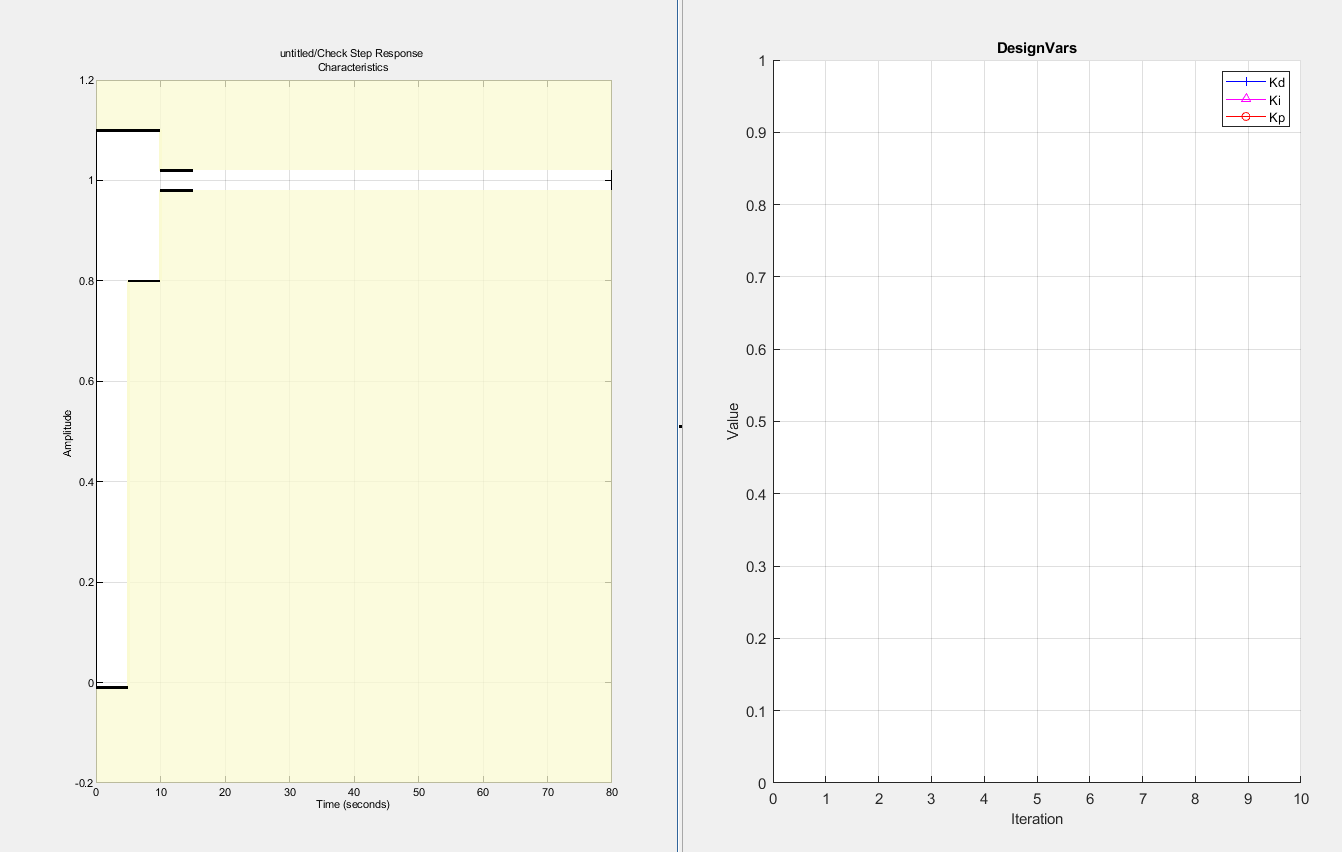

7.30. 9. Esperar a que la optimización converga#
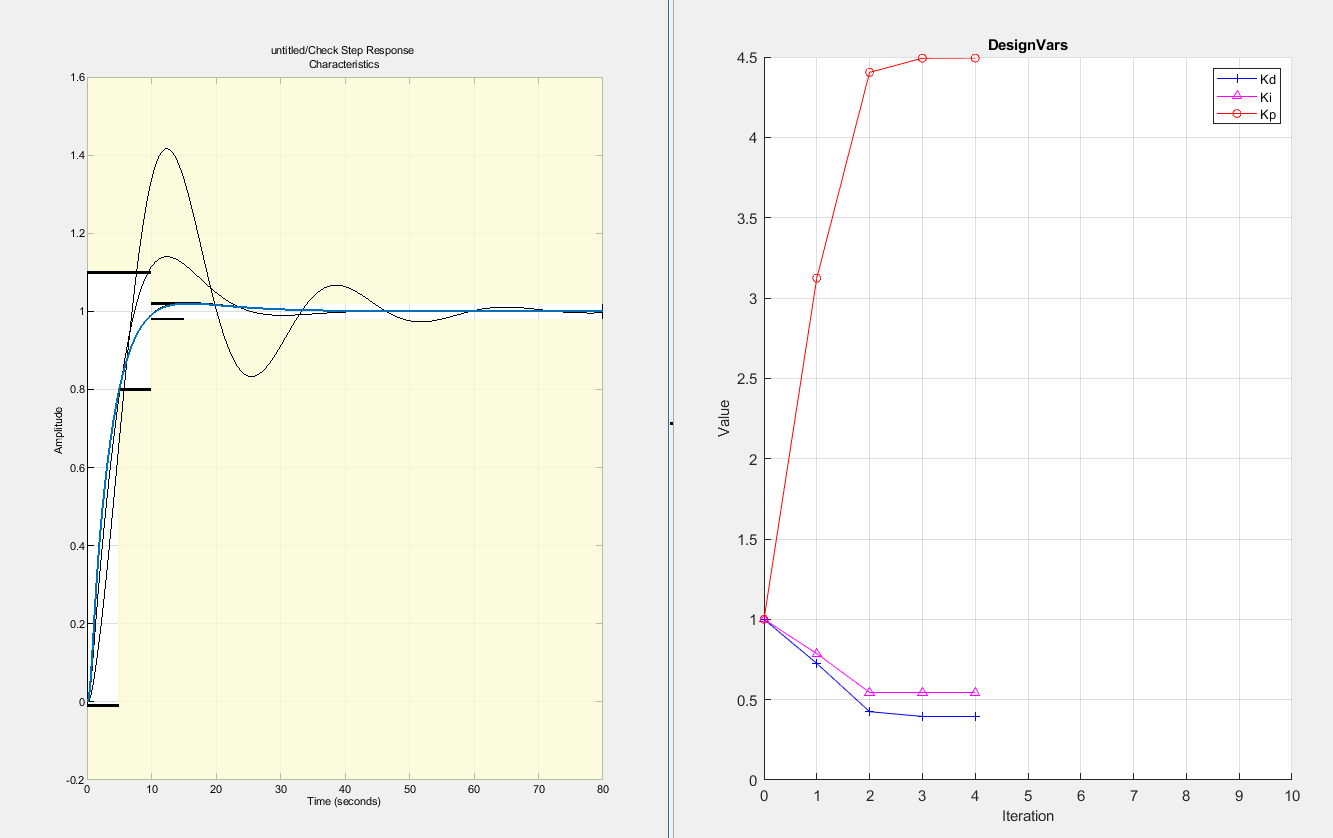
7.31. 10. Guardar los valores obtenidos#
Una vez finalizada la optimización los valores de las variables optimizadas se podrán ver en la sección de MATLAB Workspace, las variables fueron automáticamente guardadas pero es recomendable agregar los valores en el código que estemos usando para tener un respaldo.
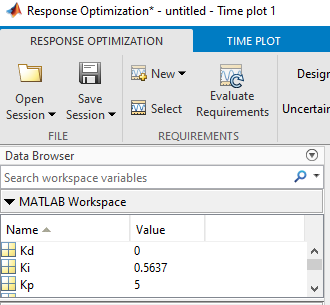
7.32. Sistema Sintonizado#
En este caso puede comprobarse que los valores obtenidos automáticamente son muy similares a los hallados con el enfoque de fuerza bruta.
A diferencia de otros métodos, en este caso uno no necesita explicitar si el controlador a utilizar será P, PD, PI o PID. Si el coeficiente es nulo, ese componente de control no se utiliza.
s = tf("s");
Kd = 0;
Ki = 0.5637;
Kp = 5;
ceros = transpose([-2]);
polos = [-3 -0.1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
controlador = Kp + Ki / s + Kd * s;
lazo_cerrado = feedback(sistema*controlador, 1);
figure;
hold on
[respuesta, t] = step(lazo_cerrado);
plot(t, respuesta)
yline(1, "--k")
xlim([0 12])
title("Salida en lazo cerrado")
grid on
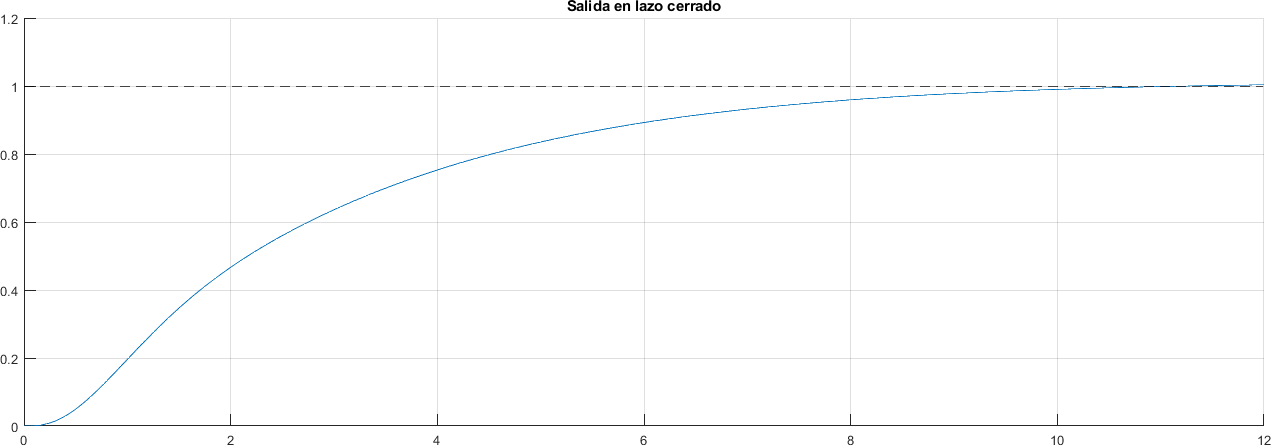
stepResults = stepinfo(respuesta, t)
stepResults =
struct with fields:
RiseTime: 5.6476
SettlingTime: 9.8380
SettlingMin: 0.9089
SettlingMax: 1.0086
Overshoot: 0
Undershoot: 0
Peak: 1.0086
PeakTime: 14.2181