Diagrama de Nyquist
Chapter Index
9. Diagrama de Nyquist#
Version 0.1
Contenido Original creado por Ezequiel Leonardo Castaño
Este contenido está INCOMPLETO y puede estar incompleto y/o sufrir modificaciones
Material faltante en este capítulo:
Impacto de un controlador en el Diagrama de Nyquist
Margen de ganancia y margen de Fase en Diagrama de Nyquist
Referencias y Recursos Adicionales
Diagrama de Nyquist en Simulink
Sintonización basada en diagrama de Nyquist en Simulink
%plot inline --format=png -w 1600 -h 800
format compact;
9.1. Diagrama de Nyquist#
El diagrama de Nyquist representa la salida del sistema para un \(K\) determinado utilizando la salida en frecuencia.
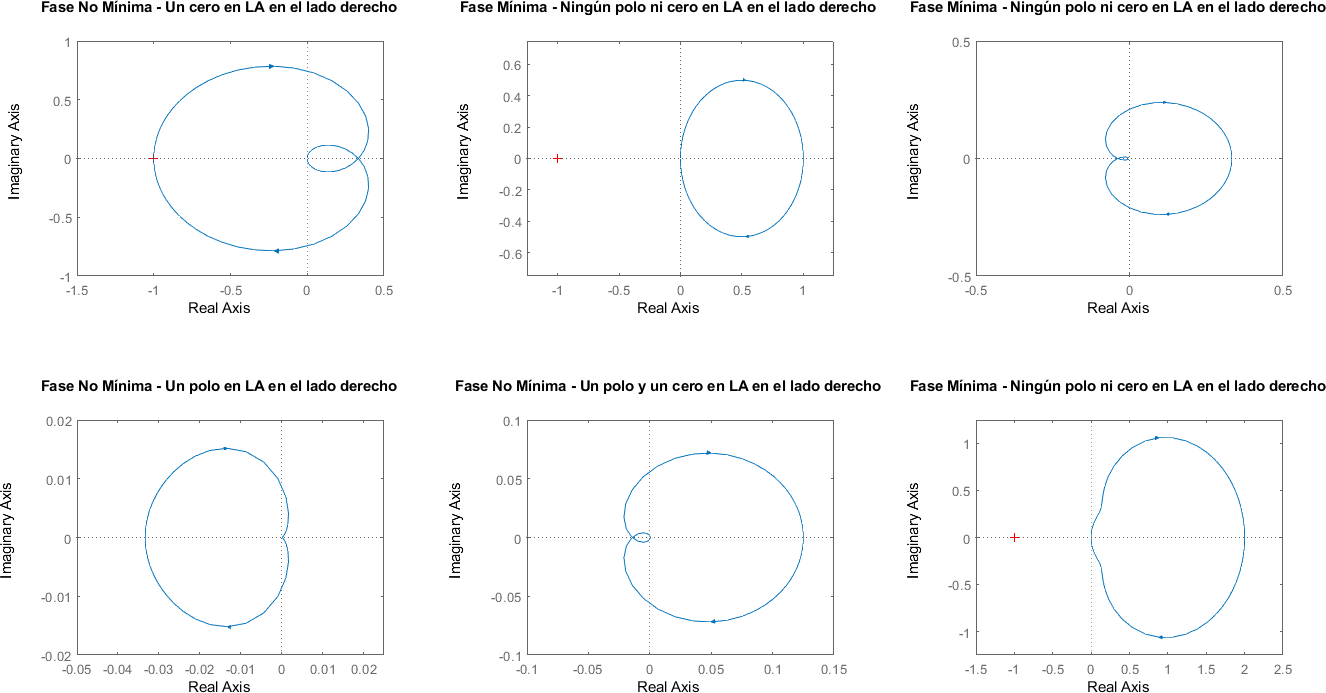
9.2. Fase Mínima vs Fase no Mínima#
Los diagramas de Nyquist pueden aplicarse tanto a sistemas de fase mínima como sistemas de fase no mínima
figure;
subplot(2, 3, 1)
sistema = zpk([2], [-1 -2], 1);
nyquist(sistema)
xlim([-1.5 0.5])
title("Fase No Mínima - Un cero en LA en el lado derecho")
subplot(2, 3, 2)
sistema = zpk([], [-1], 1);
nyquist(sistema)
xlim([-1.25 1.25])
ylim([-0.75 0.75])
title("Fase Mínima - Ningún polo ni cero en LA en el lado derecho")
subplot(2, 3, 3)
sistema = zpk([], [-1 -2 -1.5], 1);
nyquist(sistema)
xlim([-0.5 0.5])
ylim([-0.5 0.5])
title("Fase Mínima - Ningún polo ni cero en LA en el lado derecho")
subplot(2, 3, 4)
sistema = zpk([-8], [2 -5 -3 -2+2j -2-2j], 1);
nyquist(sistema)
xlim([-0.05 0.025])
ylim([-0.02 0.02])
title("Fase No Mínima - Un polo en LA en el lado derecho")
subplot(2, 3, 5)
sistema = zpk([2], [1 -1 -2 -2+2j -2-2j], 1);
nyquist(sistema)
xlim([-0.1 0.15])
ylim([-0.1 0.1])
title("Fase No Mínima - Un polo y un cero en LA en el lado derecho")
subplot(2, 3, 6)
sistema = zpk([-1+j; -1-j], [-1 -2 -0.5], 1);
nyquist(sistema)
xlim([-1.5 2.5])
ylim([-1.25 1.25])
title("Fase Mínima - Ningún polo ni cero en LA en el lado derecho")
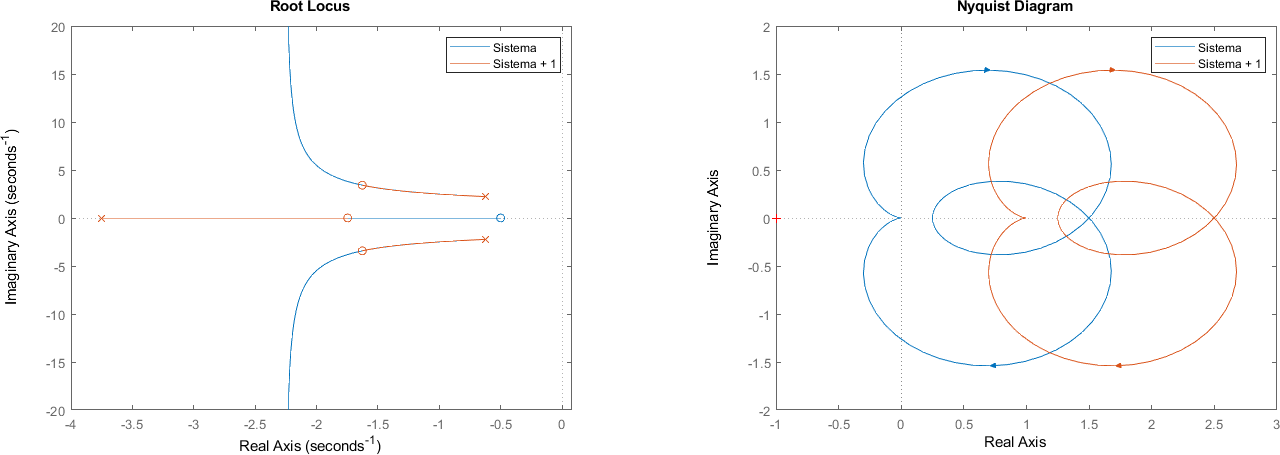
9.3. Propiedad de la suma de un escalar#
Al sumar un escalar a la función de transferencia del sistema, no es fácil predecir como van a verse afectados los polos y ceros. Sin embargo, al utilizar un diagrama de Nyquist, se produce una traslación y es más sencillo evaluar la estabilidad.
%plot inline --format=svg -w 1600 -h 500
sistema = tf([10 5], [1 5 10 20]);
figure;
subplot(1, 2, 1)
rlocus(sistema, sistema+1)
legend("Sistema", "Sistema + 1")
subplot(1, 2, 2)
nyquist(sistema, sistema+1)
legend("Sistema", "Sistema + 1")
9.4. Criterio General de Nyquist#
El criterio general de estabilidad de Nyquist puede representarse con la siguiente ecuación
\(Z\): Cantidad de **polos del sistema }a la derecha del eje imaginario
\(N\): Cantidad de rodeos al punto \((-1,0)\), si es en sentido horario es positivo y si es antihorario negativo
\(P\): Cantidad de **polos en lazo abierto} a la derecha del eje imaginario
9.4.1. Interpretación#
Si el sistema es **estable}, entonces \(Z=0\)
Si los rodeos al punto \((-1,0)\) ocurren en sentido **horario}, el sistema es inestable, ya que \(P\) no puede ser negativo.
Si el sistema es de **fase mínima}, entonces \(P=0\). Por lo tanto, para que el sistema sea estable, **no tiene que haber rodeos} al punto \((-1,0)\), es decir \(N=0\)
Si el sistema es de **fase no mínima}, pero no tiene polos en lazo abierto a la derecha del eje imaginario, entonces \(P=0\). Por lo tanto, para que el sistema sea estable, **no tiene que haber rodeos} al punto \((-1,0)\), es decir \(N=0\)
Si el sistema es de **fase no mínima }con polos a la derecha del eje imaginario, entonces \(P\not= 0\). Por lo tanto, para que el sistema sea estable se tienen que dar exactamente \(P\) rodeos al punto \((-1,0)\) en sentido **antihorario}.
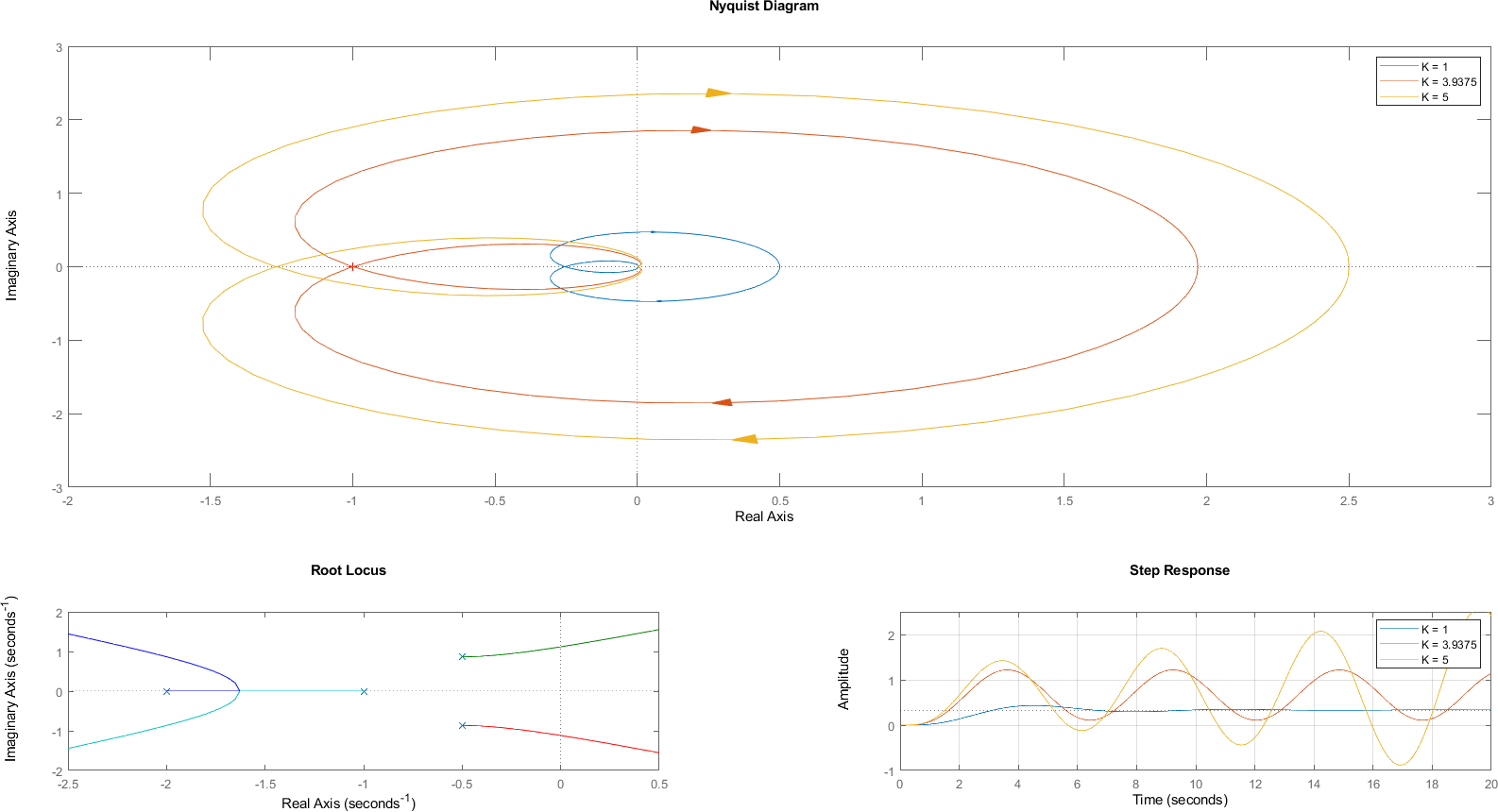
9.5. Ejemplo con Fase Mínima#
Al ser de fase mínima, \(P=0\) y para que el sistema sea estable se requiere que no haya encierros las punto \((-1,0)\).
%plot inline --format=png -w 2000 -h 1000
sistema = tf([1], [1 4 6 5 2]);
figure;
subplot(3, 2, [1 2 3 4])
nyquist(sistema, 3.9375*sistema, 5*sistema)
ylim([-3 3])
xlim([-2 3])
legend("K = 1", "K = 3.9375", "K = 5")
subplot(3, 2, 5)
rlocus(sistema)
ylim([-2 2])
xlim([-2.5 0.5])
subplot(3, 2, 6)
lazo_cerrado_1 = feedback(sistema, 1);
lazo_cerrado_2 = feedback(3.9375*sistema, 1);
lazo_cerrado_3 = feedback(5*sistema, 1);
tiempo = 0:0.02:20;
step(lazo_cerrado_1, lazo_cerrado_2, lazo_cerrado_3, tiempo )
ylim([-1 2.5])
xlim([0 20])
grid on
legend("K = 1", "K = 3.9375", "K = 5")
9.6. Ejemplo Sistema Fase No Mínima con \(P=0\)#
Al tener un cero a la derecha del eje imaginario, este sistema es de fase no mínima, pero al no tener polos en lazo abierto a la derecha del eje imaginario, \(P=0\). Por lo tanto para que el sistema sea estable es necesario que \(N=0\), esto quiere decir que no debe haber encierros al punto \((-1,0)\), ni en sentido horario ni antihorario.
[num, den] = zp2tf([2], [-2 -2+2j -2-2j], 1);
sistema = tf(num, den);
figure;
subplot(3, 2, [1 2 3 4])
frequency = logspace(-10,10, 1000);
nyquist(4*sistema, 8*sistema, 12*sistema, frequency)
xlim([-2 2])
ylim([-2 2])
legend("K = 4", "K = 8", "K = 12")
subplot(3, 2, 5)
rlocus(sistema)
xlim([-3 0.5])
ylim([-4 4])
subplot(3, 2, 6)
lazo_cerrado_1 = feedback(4*sistema, 1);
lazo_cerrado_2 = feedback(8*sistema, 1);
lazo_cerrado_3 = feedback(12*sistema, 1);
tiempo = 0:0.02:20;
step(lazo_cerrado_1, lazo_cerrado_2, lazo_cerrado_3, tiempo)
ylim([-3 0.25])
xlim([0 20])
legend("K = 4", "K = 8", "K = 12")
grid on
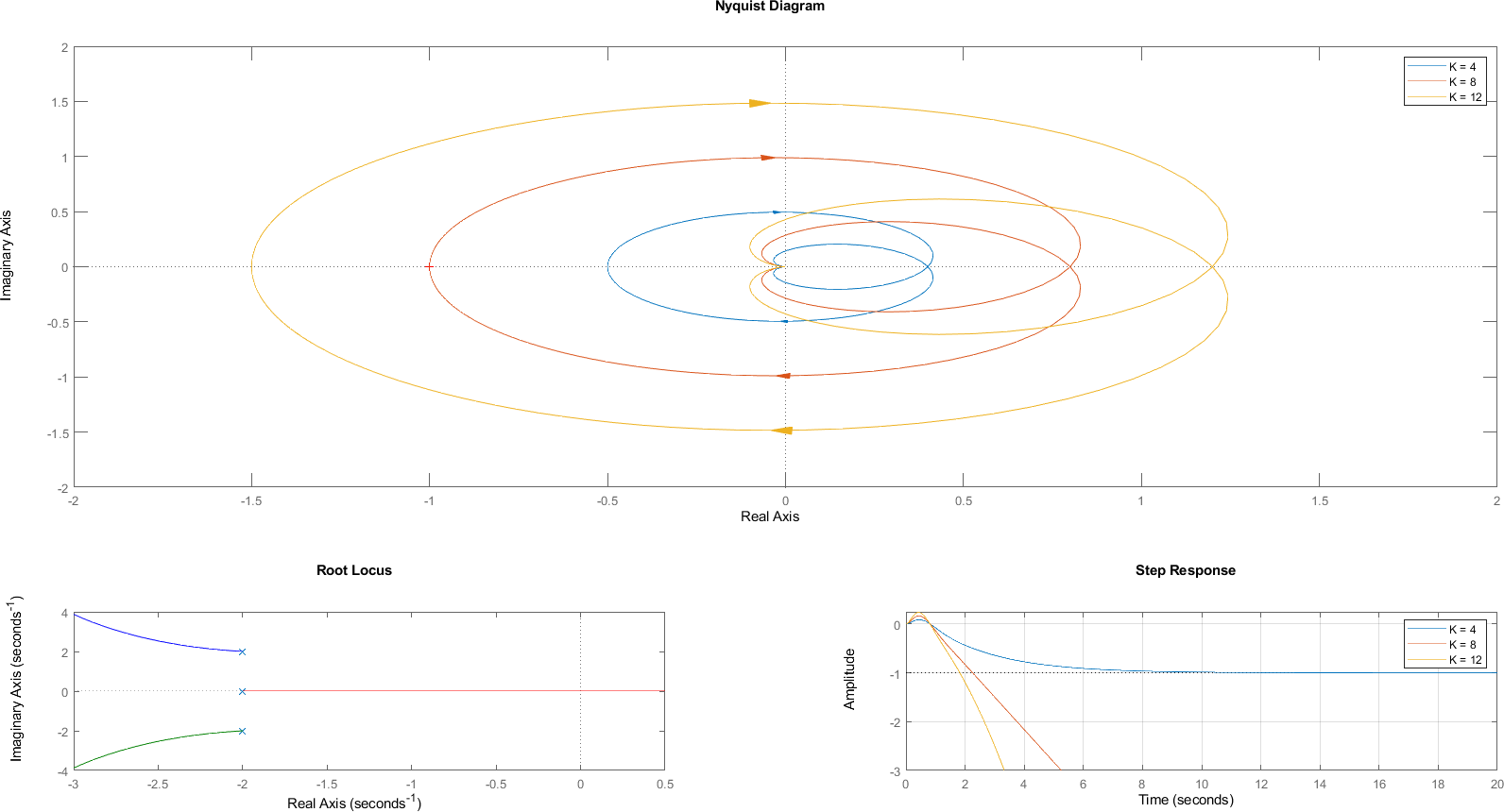
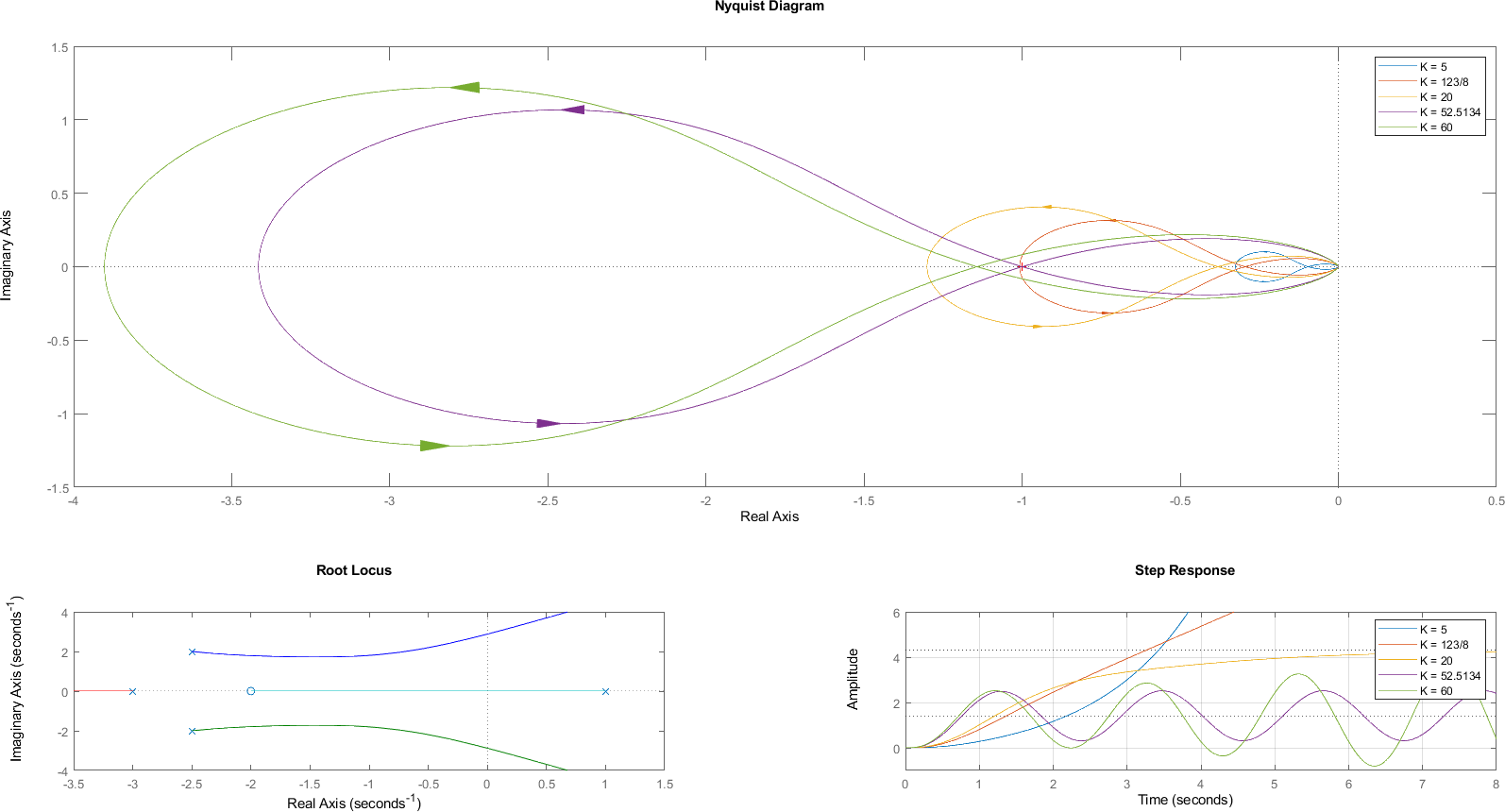
9.7. Ejemplo Sistema Fase No Mínima con \(P\not= 0\)#
En este caso \(P=1\), por lo tanto, para que el sistema sea estable es necesario que \(N=-1\), es decir, que el punto \((-1,0)\) tenga un encierro en sentido antihorario. En el Root Locus puede verse como hay dos potenciales valores críticos de \(K\), uno de ellos se encuentra en \(\frac{123}{8}\) y el otro en \(\approx 52.5134\). Se puede ver como al probar con valores de \(K\) menores y mayores, como el diagrama de Nyquist refleja la estabilidad, inestabilidad y estabilidad crítica del sistema.
ceros = transpose([-2]);
polos = [-3 1 -2.5+2j -2.5-2j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
figure;
subplot(3, 2, [1 2 3 4])
frequency = logspace(-10,10, 5000);
nyquist(5*sistema, 124/8*sistema, 20*sistema, 52.5134*sistema, 60*sistema, frequency)
xlim([-4 0.5])
ylim([-1.5 1.5])
legend("K = 5", "K = 123/8", "K = 20", "K = 52.5134", "K = 60")
subplot(3, 2, 5)
rlocus(sistema)
xlim([-3.5 1.5])
ylim([-4 4])
subplot(3, 2, 6)
lazo_cerrado_1 = feedback(5*sistema, 1);
lazo_cerrado_2 = feedback(124/8*sistema, 1);
lazo_cerrado_3 = feedback(20*sistema, 1);
lazo_cerrado_4 = feedback(52.5134*sistema, 1);
lazo_cerrado_5 = feedback(60*sistema, 1);
tiempo = 0:0.02:20;
step(lazo_cerrado_1, lazo_cerrado_2, lazo_cerrado_3, lazo_cerrado_4, lazo_cerrado_5, tiempo )
ylim([-1 6])
xlim([0 8])
grid on
legend("K = 5", "K = 123/8", "K = 20", "K = 52.5134", "K = 60")
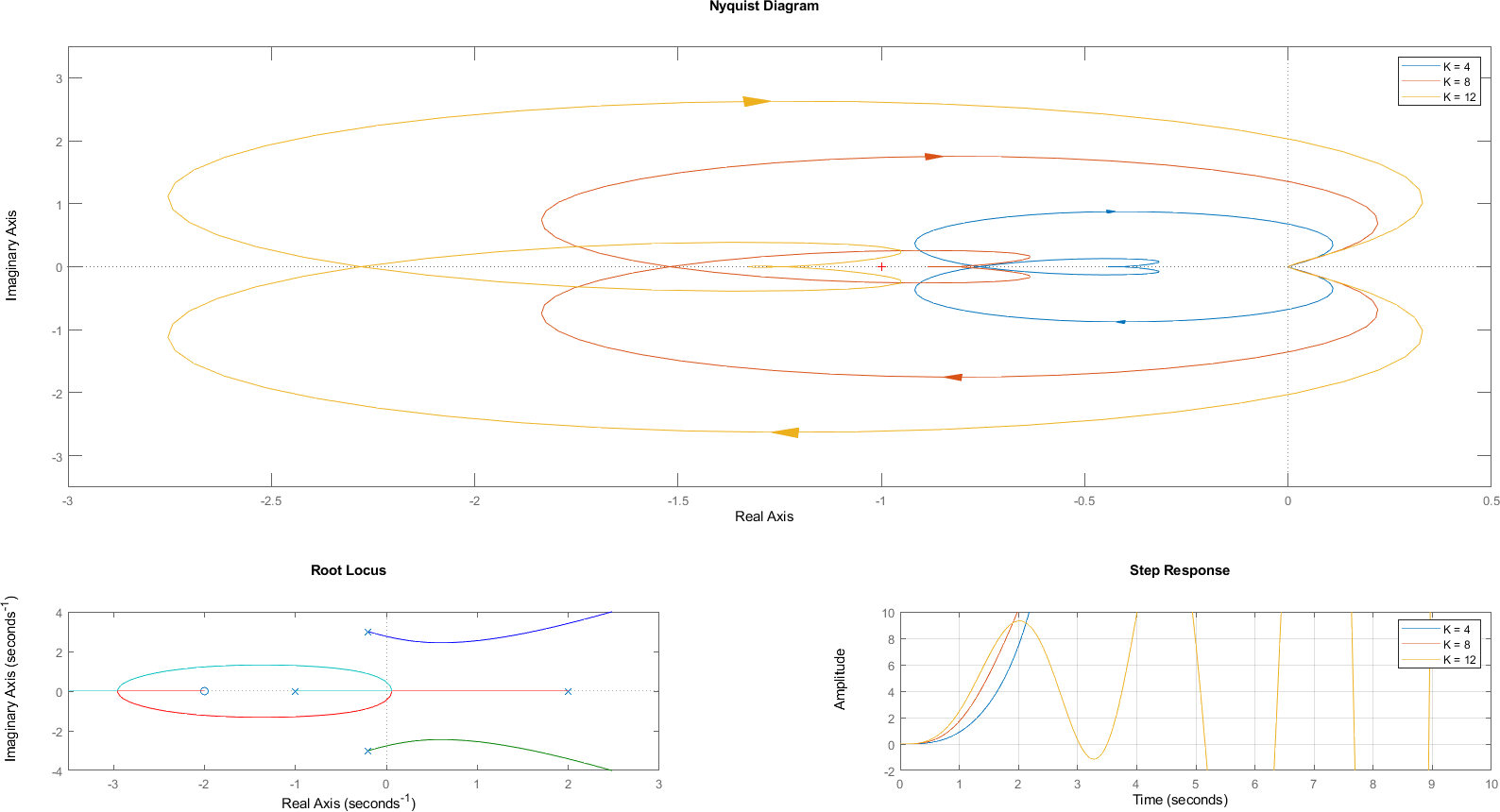
9.8. Ejemplo Sistema Inestable Fase No Mínima con \(P\not= 0\)#
En este caso \(P=1\) por lo tanto para que el sistema sea estable \(N\) tiene que ser -1, es decir, debe dar exactamente un encierro en sentido antihorario al punto \((-1,0)\). Sin embargo, como se puede ver en las gráficas, para distintos valores de \(K\) el diagrama de Nyquist tiene o 0 encierros o una cantidad positiva de encierros, ya que las curvas van siempre en sentido horario.
ceros = [-2];
polos = [-1 2 -0.2+3j -0.2-3j];
[num, den] = zp2tf(ceros, polos, [1]);
sistema = tf(num, den);
figure;
subplot(3, 2, [1 2 3 4])
nyquist(4*sistema, 8*sistema, 12*sistema)
xlim([-3 0.5])
ylim([-3.5 3.5])
legend("K = 4", "K = 8", "K = 12")
subplot(3, 2, 5)
rlocus(sistema)
xlim([-3.5 3])
ylim([-4 4])
subplot(3, 2, 6)
lazo_cerrado_1 = feedback(4*sistema, 1);
lazo_cerrado_2 = feedback(8*sistema, 1);
lazo_cerrado_3 = feedback(12*sistema, 1);
tiempo = 0:0.02:20;
step(lazo_cerrado_1, lazo_cerrado_2, lazo_cerrado_3, tiempo )
ylim([-2 10])
xlim([0 10])
legend("K = 4", "K = 8", "K = 12")
grid on