Sistemas de Primer Orden
Chapter Index
3. Sistemas de Primer Orden#
Version 0.1
Contenido Original creado por Ezequiel Leonardo Castaño
Este contenido está INCOMPLETO y puede estar incompleto y/o sufrir modificaciones
Material faltante en este capítulo:
Representación en Simulink
Sistema de primer orden en Lazo Cerrado
Interpretación como filtro paso bajo de un sistema de primer orden
%plot inline --format=png -w 1600 -h 500
format compact;
3.1. Sistemas de Primer Orden#
Al utilizarse sistemas de primer orden, si la función de transferencia es propia, entonces su forma está definida por
Esto es así ya que \(Y(s)\)no puede contener términos de grado mayor a \(2\) ya que eso implicaría derivadas de grado \(2\) o superior. Y si el sistema es propio, esto implica que el numerador no puede tener un grado mayor al denominador.
Se tienen dos casos, cuando \(G\) tiene un cero y cuando no tiene ningún cero
La forma con un cero suele representarse como
Y la forma sin cero suele representarse como:
\(G=k\frac{p}{s+p}\) o también \(G=k\frac{1}{\frac{s}{p}+1}\)
En este caso al valor \(\frac{1}{p}\) se le conoce como **constante de tiempo} y se representa con \(\tau\) quedando
3.2. Polos y Ceros#
3.3. Lazo Abierto y Lazo Cerrado#
3.4. Funciones de transferencia en Matlab#
En matlab existen diversas formas de declarar funciones de transferencia
Declarando la variable compleja \(s\)
Usando la variable compleja \(s\) pueden especificarse las funciones de transferencia como cociente de polinomios, como polos y ceros o una combinación de ambos
s = tf("s");
sistema = ((s+2)*(s+1)) / ((s+2)*(s+1)*(s+1.5)) % Polos y Ceros
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
sistema = (s^2 + 3*s + 2) / (s^3 + 4.5*s^2 + 6.5*s + 3) % Cociente de Polinomios
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
sistema = (s^2 + 3*s + 2) / ((s+2)*(s+1)*(s+1.5)) % Combinación
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
Especificando los coeficientes del numerador y denominador
Para utilizar sólamente los coeficientes del numerador y el denominador, se utiliza la función tf.
sistema = tf([1 3 2], [1 4.5 6.5 3])
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
Especificando los polos y ceros
Para definir la función de transferencia con polos y ceros, se utiliza la función zpk, que además toma un tercer parámetro que es la ganancia
sistema = zpk([-2; -1], [-2, -1, -1.5], 1)
sistema =
(s+2) (s+1)
-------------------
(s+2) (s+1.5) (s+1)
Continuous-time zero/pole/gain model.
3.5. Ceros y polos de una función de transferencia#
Independientemente de la forma en la que la función de transferencia haya sido creada, es posible obtener sus ceros y polos con las funciones zero y pole
ceros = zero(sistema);
polos = pole(sistema);
ceros, polos
ceros =
-2
-1
polos =
-2.0000
-1.0000
-1.5000
3.6. Convirtiendo de un formato a otro#
De ceros y polos a coeficientes usando zp2tf
ceros = [-2; -1];
polos = [-2, -1, -1.5];
sistema = zpk(ceros, polos, 1)
sistema =
(s+2) (s+1)
-------------------
(s+2) (s+1.5) (s+1)
Continuous-time zero/pole/gain model.
[numerador, denominador] = zp2tf(ceros, polos, 1);
sistema = tf(numerador, denominador)
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
De cociente de polinomios a polos y ceros tf2zp
numerador = [1 3 2];
denominador = [1 4.5 6.5 3];
sistema = tf(numerador, denominador)
sistema =
s^2 + 3 s + 2
-------------------------
s^3 + 4.5 s^2 + 6.5 s + 3
Continuous-time transfer function.
[polos, ceros, ganancia] = tf2zp(numerador, denominador);
sistema = zpk(polos, ceros, ganancia)
sistema =
(s+2) (s+1)
-------------------
(s+2) (s+1.5) (s+1)
Continuous-time zero/pole/gain model.
3.7. Respuesta del sistema#
La respuesta del sistema \(y(t)\)está totalmente definida dada la función de transferencia \(G\) y una entrada \(x(t)\)
A continuación se muestra como un sistema de primer orden responde a diferentes tipos de entrada
3.7.1. Definiendo el sistema#
Primero se define la variable compleja \(s\) y un sistema de primer orden sin ceros y con un polo en \(p\)
s = tf("s");
tiempo = 0:0.01:2;
tau =0.2;
primer_orden = 1 / (tau*s + 1);
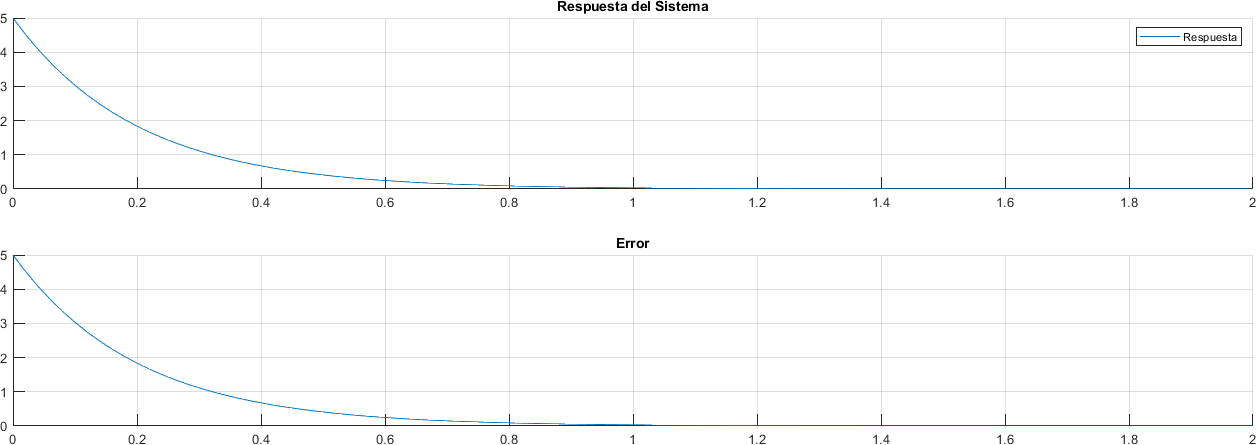
3.7.2. Entrada Impulso#
respuesta = impulse(primer_orden, tiempo);
figure;
ax = subplot(2,1,1);
hold(ax, 'on')
plot(ax, tiempo, transpose(respuesta))
legend('Respuesta')
title("Respuesta del Sistema")
grid on
ax = subplot(2,1,2);
hold(ax, 'on')
plot(tiempo, respuesta)
title("Error")
grid on
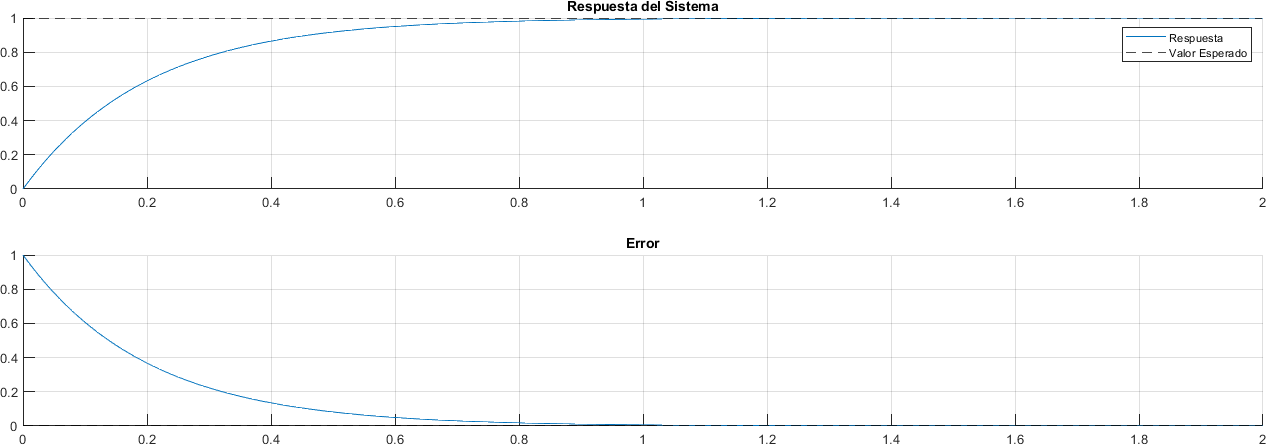
3.7.3. Entrada Escalón#
valor_esperado = 1;
respuesta = step(valor_esperado * primer_orden, tiempo);
figure;
ax = subplot(2,1,1);
hold(ax, 'on')
plot(ax, tiempo, transpose(respuesta))
yline(ax, valor_esperado, "--k")
legend('Respuesta', 'Valor Esperado')
title("Respuesta del Sistema")
grid on
ax = subplot(2,1,2);
hold(ax, 'on')
plot(tiempo, valor_esperado - respuesta)
yline(0, "--k")
title("Error")
grid on
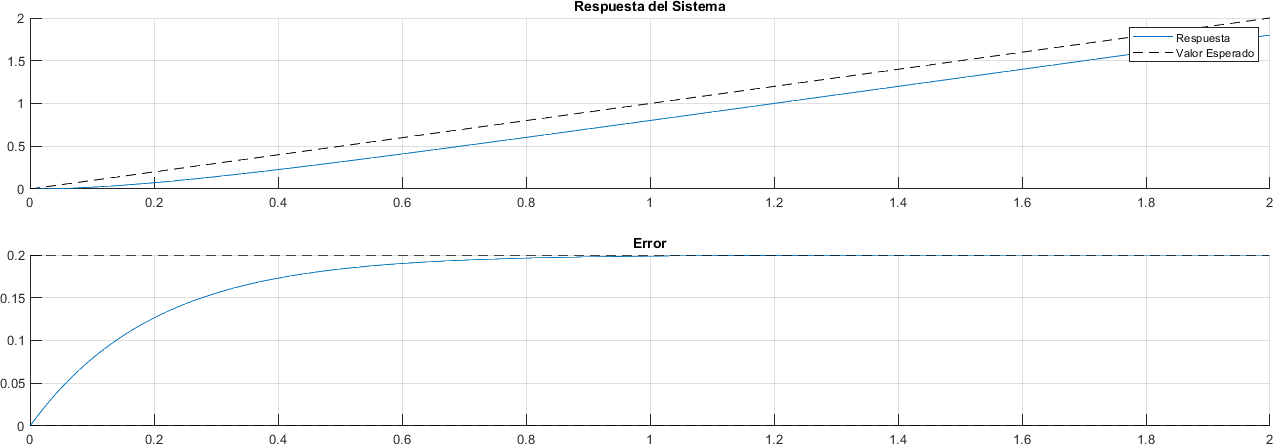
3.7.4. Entrada Rampa#
valor_esperado = tiempo;
respuesta = step(primer_orden / s, tiempo);
respuesta = transpose(respuesta);
figure;
ax = subplot(2,1,1);
hold(ax, 'on')
plot(ax, tiempo, respuesta)
plot(ax, tiempo, valor_esperado, "--k")
legend('Respuesta', 'Valor Esperado')
grid on
title("Respuesta del Sistema")
ax = subplot(2,1,2);
hold(ax, 'on')
error = valor_esperado - respuesta;
plot(tiempo, error)
yline(error(end), "--k")
yline(0, "--k")
title("Error")
grid on
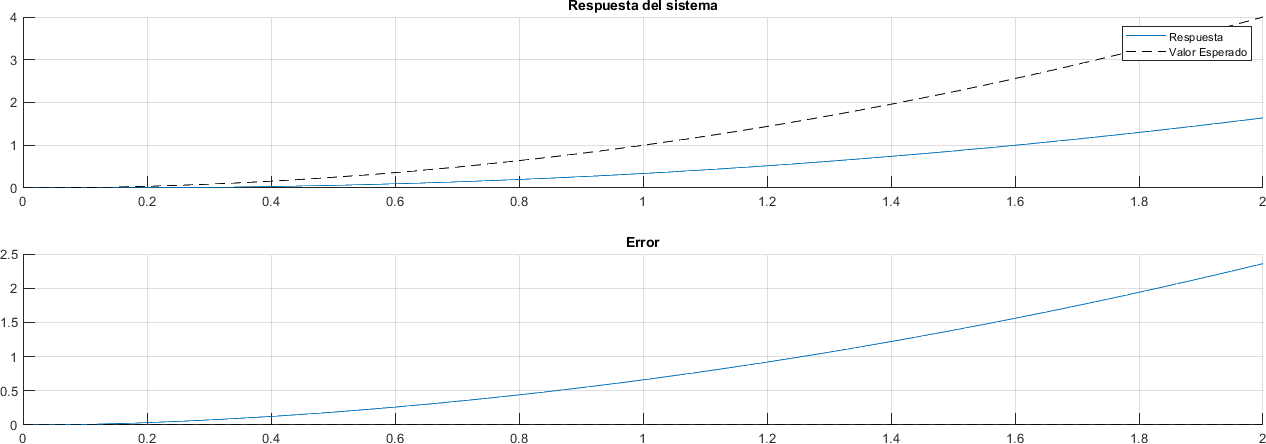
3.7.5. Entrada Parabola#
En este caso, si la entrada es una parábola, se puede ver como el error crece a infinito
valor_esperado = tiempo .* tiempo;
respuesta = step(primer_orden / s^2, tiempo);
respuesta = transpose(respuesta);
figure;
ax = subplot(2,1,1);
hold(ax, 'on')
plot(ax, tiempo, respuesta)
plot(ax, tiempo, valor_esperado, "--k")
legend('Respuesta', 'Valor Esperado')
title("Respuesta del sistema")
grid on
ax = subplot(2,1,2);
hold(ax, 'on')
plot(tiempo, valor_esperado - respuesta)
yline(0, "--k")
title("Error")
grid on