5. Root Locus#

Version 0.1

Contenido Original creado por Ezequiel Leonardo Castaño

Este contenido está INCOMPLETO y puede estar incompleto y/o sufrir modificaciones

Material faltante en este capítulo:

  • Cálculo del punto de ruptura

  • Cálculo del ángulo de partida

  • Cálculo del punto de interseccion de las asíntotas

  • Cálculo del punto de interseccion con el eje imaginario (ganancia crítica)

%plot inline --format=png -w 1600 -h 800

format compact;

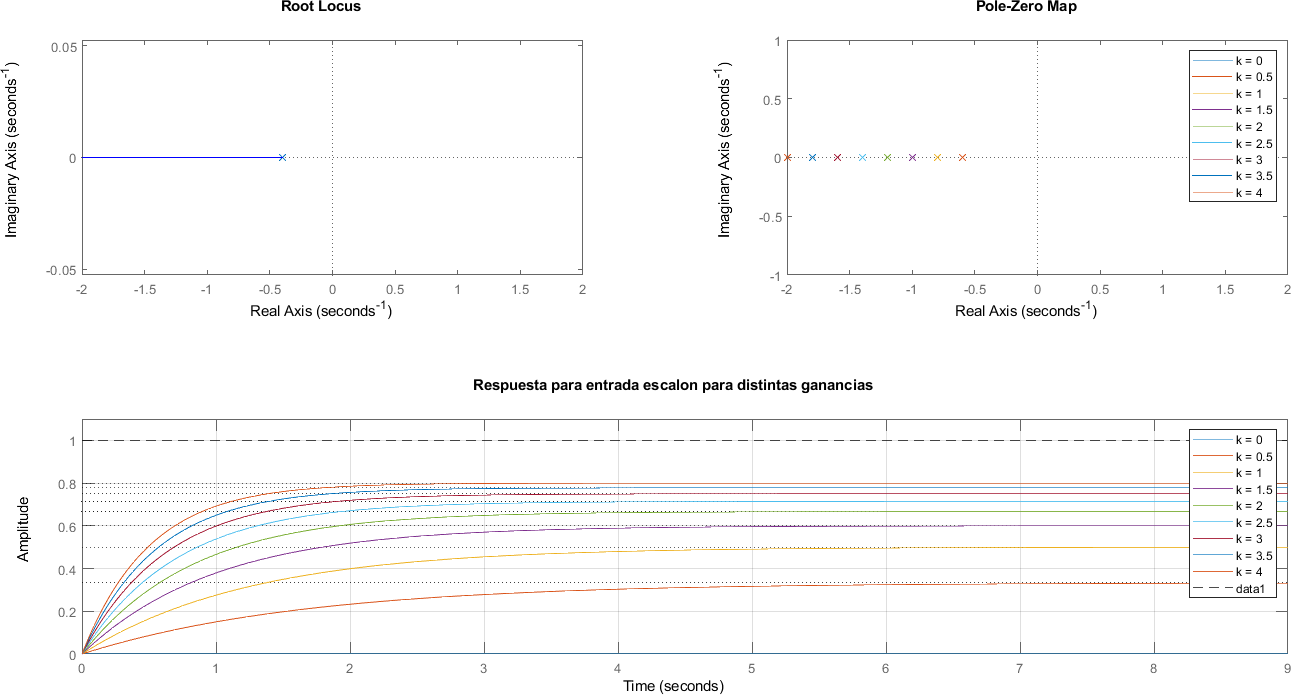
5.1. Sistemas de Primer Orden sin cero#

p = 0.4;
ganancia_valores = 0:0.5:4;
s = tf("s");

primer_orden = p/(s+p);

figure;
subplot(2,2,1);
rlocus(primer_orden)
xlim([-2 2]);


ax = subplot(2,2,2);
hold(ax, "on")
for index = 1:length(ganancia_valores)
    k = ganancia_valores(index);
    lazo_cerrado = feedback(k*primer_orden, 1);
    pzmap(lazo_cerrado)
    legendInfo{index} = ['k = ' num2str(k)]; 
end
legend(legendInfo)
xlim([-2 2]);


ax = subplot(2, 2, [3, 4]);
hold(ax, "on")

for index = 1:length(ganancia_valores)
    k = ganancia_valores(index);
    step(feedback(k*primer_orden, 1))
    legendInfo{index} = ['k = ' num2str(k)]; 
end

legend(legendInfo)
title("Respuesta para entrada escalon para distintas ganancias")
yline(1, "--k")
ylim([0, 1.1])
xlim([0 9])
grid on
../_images/ELC05_Root_Locus_4_1.png

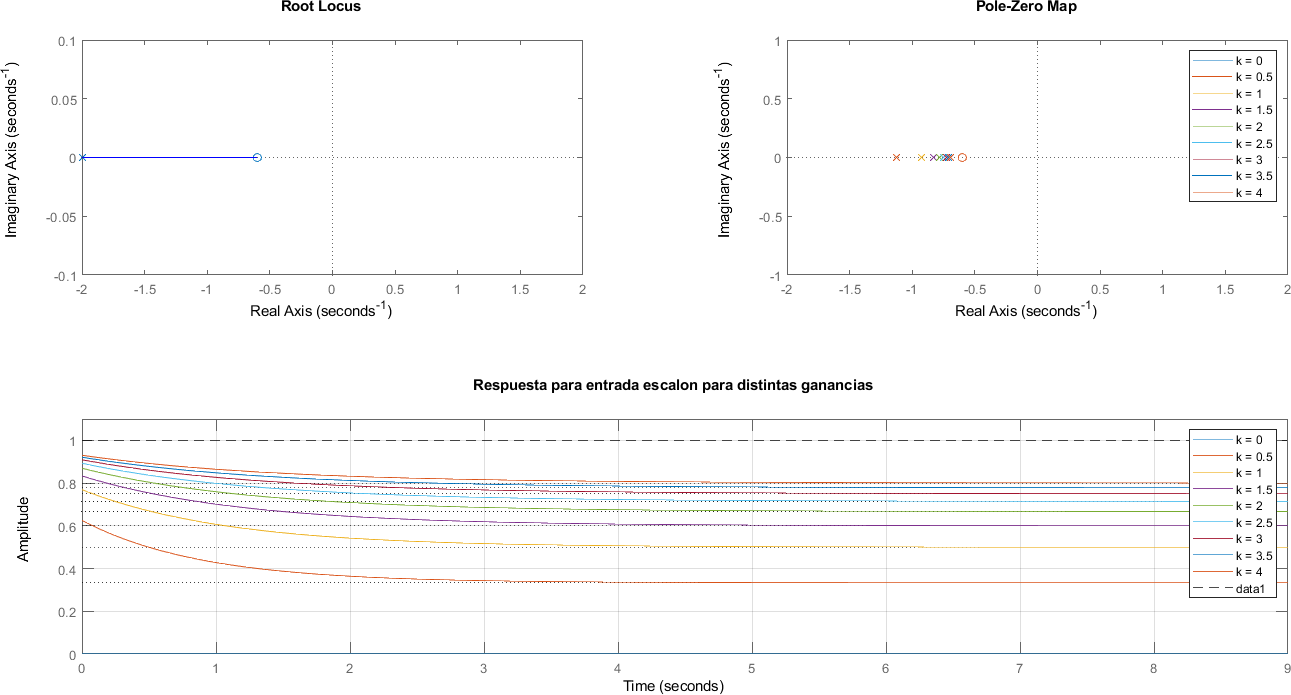
5.2. Sistemas de Primer Orden con un cero#

p = 2;
z = 0.6;
ganancia_valores = 0:0.5:4;
s = tf("s");

primer_orden = p/z * (s+z)/(s+p);

figure;
subplot(2,2,1);
rlocus(primer_orden)
xlim([-2 2]);


ax = subplot(2,2,2);
hold(ax, "on")
for index = 1:length(ganancia_valores)
    k = ganancia_valores(index);
    lazo_cerrado = feedback(k*primer_orden, 1);
    pzmap(lazo_cerrado)
    legendInfo{index} = ['k = ' num2str(k)]; 
end
legend(legendInfo)
xlim([-2 2]);


ax = subplot(2, 2, [3, 4]);
hold(ax, "on")

for index = 1:length(ganancia_valores)
    k = ganancia_valores(index);
    step(feedback(k*primer_orden, 1))
    legendInfo{index} = ['k = ' num2str(k)]; 
end

legend(legendInfo)
title("Respuesta para entrada escalon para distintas ganancias")
yline(1, "--k")
ylim([0, 1.1])
xlim([0 9])
grid on
../_images/ELC05_Root_Locus_6_1.png

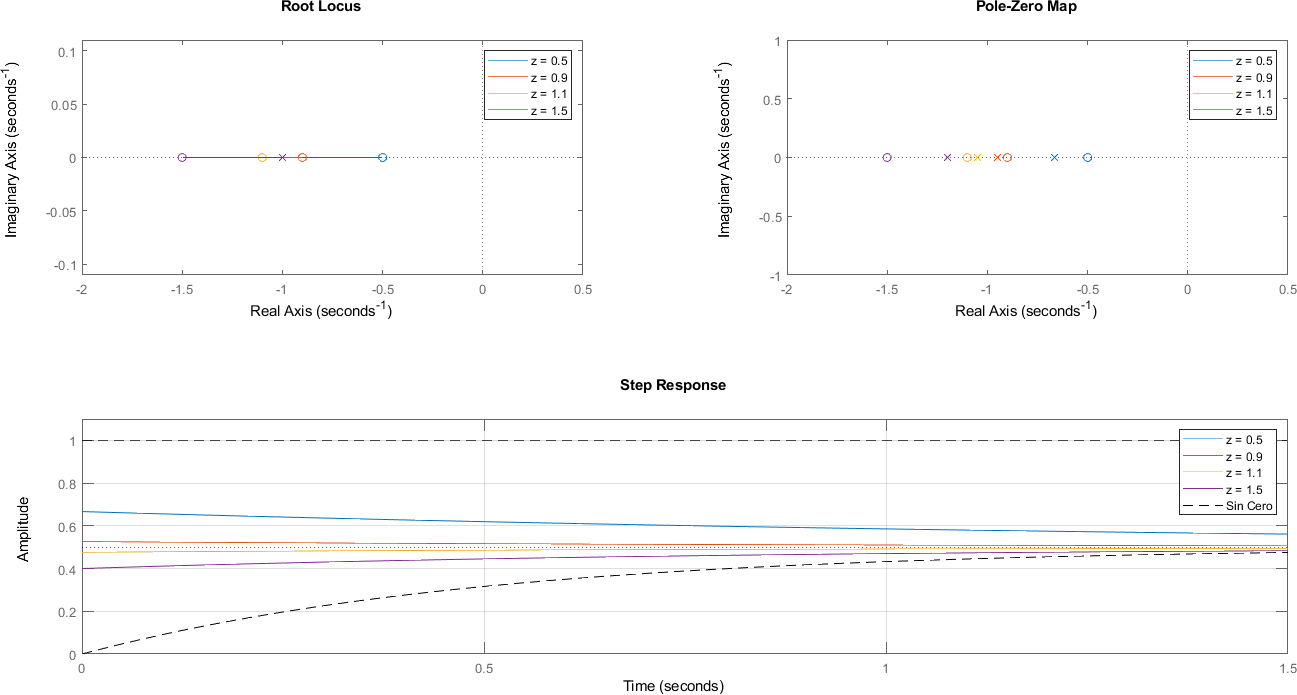
5.3. Casos#

p = 1;
k = 1;

s = tf("s");

figure;
valores_ceros = [0.5 0.9 1.1 1.5];
for index = 1:length(valores_ceros)
    z = valores_ceros(index);
    primer_orden = p/z * (s+z)/(s+p);
    primer_orden_{index} = primer_orden;
    lazo_cerrado_{index} = feedback(k*primer_orden, 1);
    legend_info{index} = ['z = ' num2str(z)];
end

ax1 = subplot(2,2,1);
rlocus(primer_orden_{:})
xlim([-2 0.5]);


ax2 = subplot(2,2,2);
pzmap(lazo_cerrado_{:})
xlim([-2 0.5]);


ax3 = subplot(2, 2, [3, 4]);
hold(ax3, "on")
step(lazo_cerrado_{:})

primer_orden = p/(s+p);
[respuesta, tiempo] = step(feedback(k*primer_orden, 1));
plot(tiempo, respuesta, "--k")

yline(1, "--k")
ylim([0, 1.1])
xlim([0 1.5])
grid on

legend(ax1, legend_info)
legend(ax2, legend_info)

legend_info{index+1} = "Sin Cero";
legend(ax3, legend_info)
../_images/ELC05_Root_Locus_8_1.png

5.4. Sistemas de Segundo Orden sin cero#

%plot inline --format=png -w 1600 -h 500

omega = 1;
zeta =0.5;

s = tf("s");
segundo_orden = omega^2 / (s^2 + 2*omega*zeta*s + omega^2);

figure;
hold on
rlocus(segundo_orden)
m = tan(acos(zeta)); 
x = linspace(-1.5, 0);
plot(x, m*x, '--', "Color", [0 0 0])
plot(x, -m*x, '--', "Color", [0 0 0])

th = 1/2*pi:pi/50:3/2*pi;
xunit = omega * cos(th);
yunit = omega * sin(th);
h = plot(xunit, yunit, "--k");

xlim([-1.5 0.2])
ylim([-2 2])
grid on
../_images/ELC05_Root_Locus_11_1.png

Lugar geométrico de las raices para distintos valores de omega

%plot inline --format=png -w 1600 -h 800

k = 1;

omega_values = [0.10, 0.25, 0.50, 0.75, 1.00];
legendInfo = {};
for index = 1:length(omega_values)
    omega_ = omega_values(index);
    segundo_orden = (omega_^2) / (s^2 + 2*omega_*zeta*s + omega_^2);
    segundo_orden_{index} = segundo_orden;
    lazo_cerrado_{index} = feedback(k * segundo_orden, 1);
    legendInfo{index} = ['\omega = ' num2str(omega_)]; 
end

figure;
ax1 = subplot(2,2,1);
hold(ax1, "on")
rlocus(segundo_orden_{:})
m = tan(acos(zeta)); 
x = linspace(-1, 0);
plot(x, m*x, '--', "Color", [0 0 0])
plot(x, -m*x, '--', "Color", [0 0 0])
xlim([-1 0.2])
ylim([-1 1])
legend(ax1, legendInfo, 'AutoUpdate', 'off')
title("Lugar Geométrico de las Raices variando \omega")


ax2 = subplot(2,2,3);
hold(ax2, "on")
step(lazo_cerrado_{:})
legend(ax2, legendInfo, 'AutoUpdate', 'off')
title("Respuesta a entrada escalón variando \omega")
grid on

zeta_values = [0.25, 0.50, 0.75, 1.00, 1.5];
for index = 1:length(zeta_values)
    zeta_ = zeta_values(index);
    segundo_orden = (omega^2) / (s^2 + 2*omega*zeta_*s + omega^2);
    segundo_orden_{index} = segundo_orden;
    lazo_cerrado_{index} = feedback(k * segundo_orden, 1);
    legendInfo{index} = ['\zeta = ' num2str(zeta_)]; 
end

ax2 = subplot(2,2,2);
hold(ax2, "on")
rlocus(segundo_orden_{:})

th = 1/2*pi:pi/50:3/2*pi;
xunit = omega * cos(th);
yunit = omega * sin(th);
h = plot(xunit, yunit, "--k");

xlim([-3 0.8])
ylim([-2 2])
legend(ax2, legendInfo, 'AutoUpdate', 'off')
title("Lugar Geométrico de las Raices variando \zeta")


ax4 = subplot(2,2,4);
hold(ax2, "on")
step(lazo_cerrado_{:})
legend(ax4, legendInfo, 'AutoUpdate', 'off')
title("Respuesta a entrada escalón variando \zeta")
grid on
../_images/ELC05_Root_Locus_14_1.png

5.5. Sistemas de Segundo Orden con un cero#

%plot inline --format=png -w 1600 -h 500

omega = 1;
zeta =0.1;
z = 0.9;

s = tf("s");
segundo_orden = (omega^2*(s/z+1)) / (s^2 + 2*omega*zeta*s + omega^2);

figure;
hold on;
rlocus(segundo_orden)

m = tan(acos(zeta)); 
x = linspace(-1, 0);
plot(x, m*x, '--', "Color", [0 0 0])
plot(x, -m*x, '--', "Color", [0 0 0])

th = 1/2*pi:pi/50:3/2*pi;
xunit = omega * cos(th);
yunit = omega * sin(th);
h = plot(xunit, yunit, "--k");
xlim([-3 0.5])
ylim([-4 4])
grid on
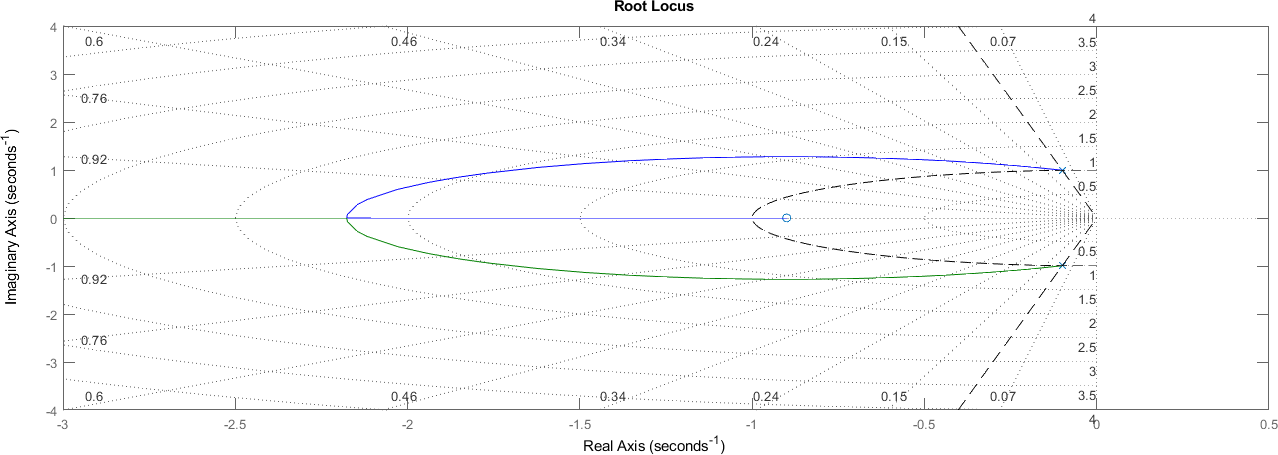
../_images/ELC05_Root_Locus_17_1.png

5.5.1. Caso 1: Polos Reales#

%plot inline --format=png -w 1600 -h 800

omega = 1;
zeta = 1.5;
k = 1;

s = tf("s");

figure;
valores_ceros = [0.25 0.5 1.5 3];
for index = 1:length(valores_ceros)
    z = valores_ceros(index);
    segundo_orden = (omega^2*(s/z+1)) / (s^2 + 2*omega*zeta*s + omega^2);
    segundo_orden_{index} = segundo_orden;
    lazo_cerrado_{index} = feedback(k*segundo_orden, 1);
    legend_info{index} = ['z = ' num2str(z)];
end

ax1 = subplot(2,2,1);
rlocus(segundo_orden_{:})
%xlim([-3 0.5]);

ax2 = subplot(2,2,2);
pzmap(segundo_orden_{:})
%xlim([-3 0.5]);

ax3 = subplot(2, 2, [3, 4]);
hold(ax3, "on")
step(lazo_cerrado_{:})

segundo_orden = omega^2 / (s^2 + 2*omega*zeta*s + omega^2);
[respuesta, tiempo] = step(feedback(segundo_orden, 1));
plot(tiempo, respuesta, "--k")

yline(1, "--k")
ylim([0, 1.2])
xlim([0 5])
grid on

legend(ax1, legend_info)
legend(ax2, legend_info)
legend_info{index+1} = "Sin Cero";
legend(ax3, legend_info)
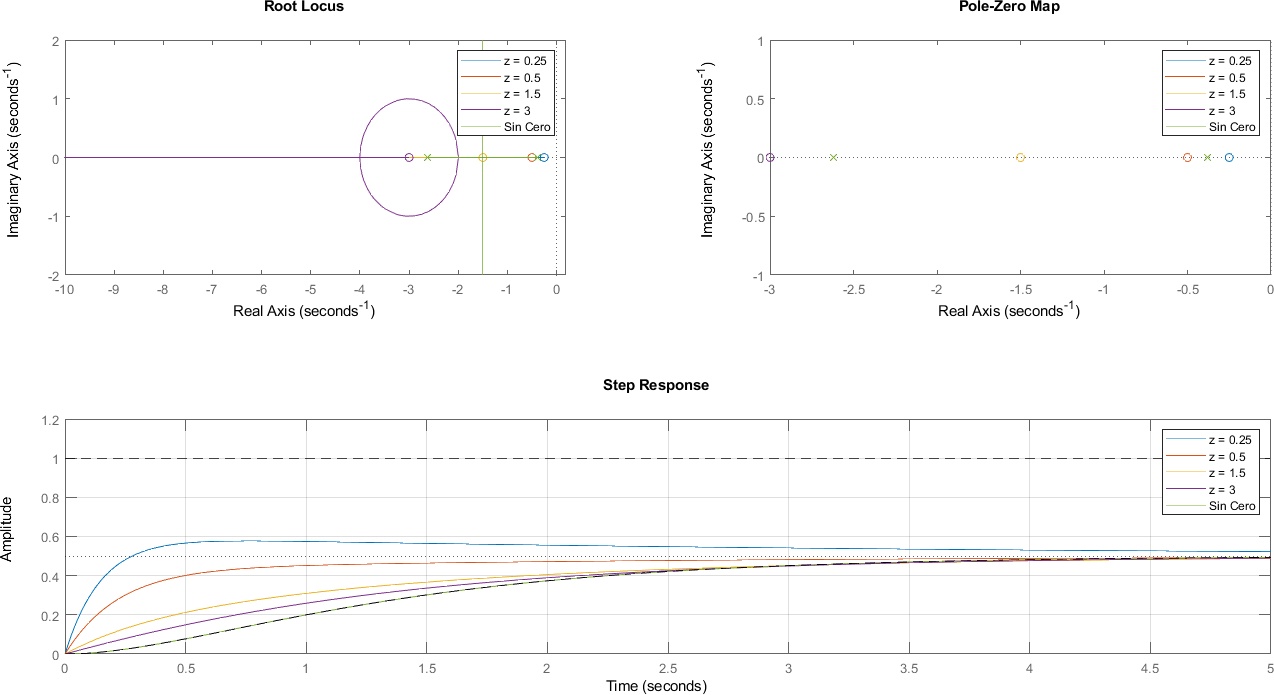
../_images/ELC05_Root_Locus_20_1.png

5.5.2. Caso 2: Polos Complejos#

omega = 1;
zeta = 0.5;
k = 1;

s = tf("s");

figure;
valores_ceros = [0.25 0.5 1.5 5];
for index = 1:length(valores_ceros)
    z = valores_ceros(index);
    segundo_orden = (omega^2*(s/z+1)) / (s^2 + 2*omega*zeta*s + omega^2);
    segundo_orden_{index} = segundo_orden;
    lazo_cerrado_{index} = feedback(k*segundo_orden, 1);
    legend_info{index} = ['z = ' num2str(z)];
end

ax1 = subplot(2,2,1);
rlocus(segundo_orden_{:})
%xlim([-3 0.5]);

ax2 = subplot(2,2,2);
pzmap(segundo_orden_{:})
%xlim([-3 0.5]);

ax3 = subplot(2, 2, [3, 4]);
hold(ax3, "on")
step(lazo_cerrado_{:})

segundo_orden = omega^2 / (s^2 + 2*omega*zeta*s + omega^2);
[respuesta, tiempo] = step(feedback(segundo_orden, 1));
plot(tiempo, respuesta, "--k")

yline(1, "--k")
ylim([0, 1.2])
xlim([0 5])
grid on

legend(ax1, legend_info)
legend(ax2, legend_info)
legend_info{index+1} = "Sin Cero";
legend(ax3, legend_info)
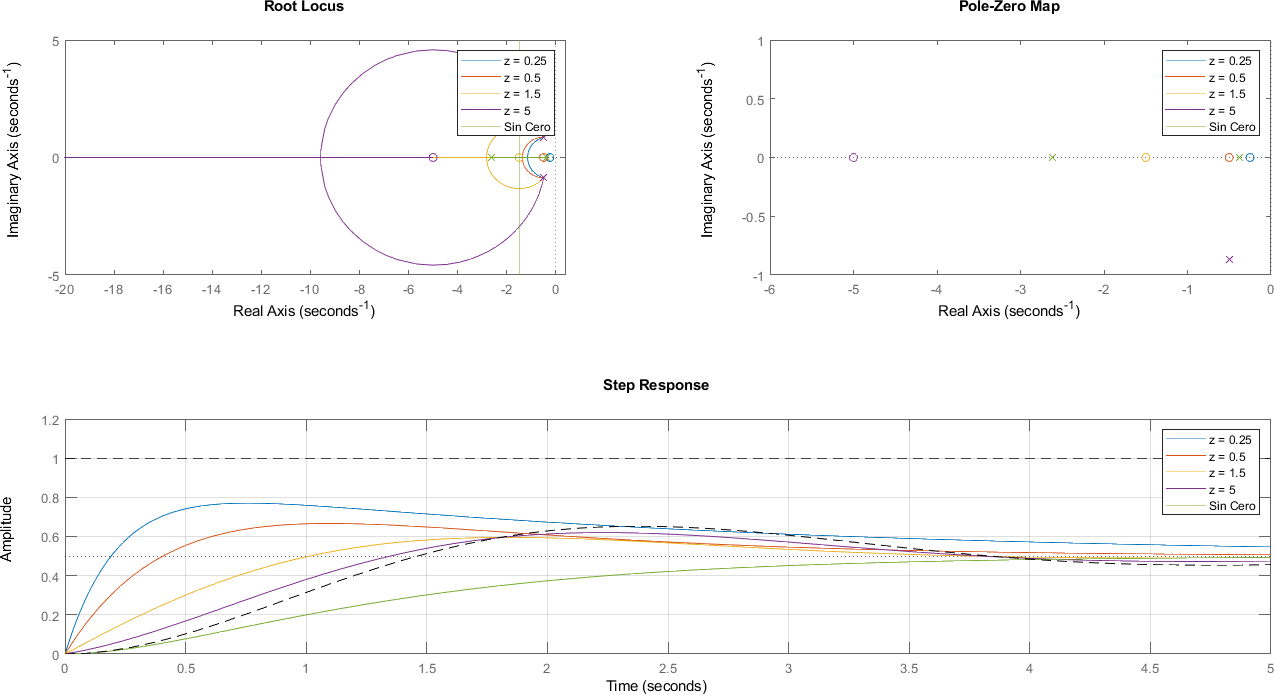
../_images/ELC05_Root_Locus_22_1.png

5.7. En Lazo Abierto#

Este sistema contiene una función de transferencia propia y sus polos y ceros pueden hallarse con las funciones zero y pole:

s = tf("s");
sistema = (s^2 + 2*s + 2) / (s^3 + 4*s^2 + 3*s);
ceros = zero(sistema);
polos = pole(sistema);

ceros, polos

ceros =
  -1.0000 + 1.0000i
  -1.0000 - 1.0000i
polos =
     0
    -3
    -1

Al usar Matlab, graficar estos ceros y polos es sencillo utilizando la función pzmap

%plot inline --format=png -w 1600 -h 500

pzmap(sistema)
grid on
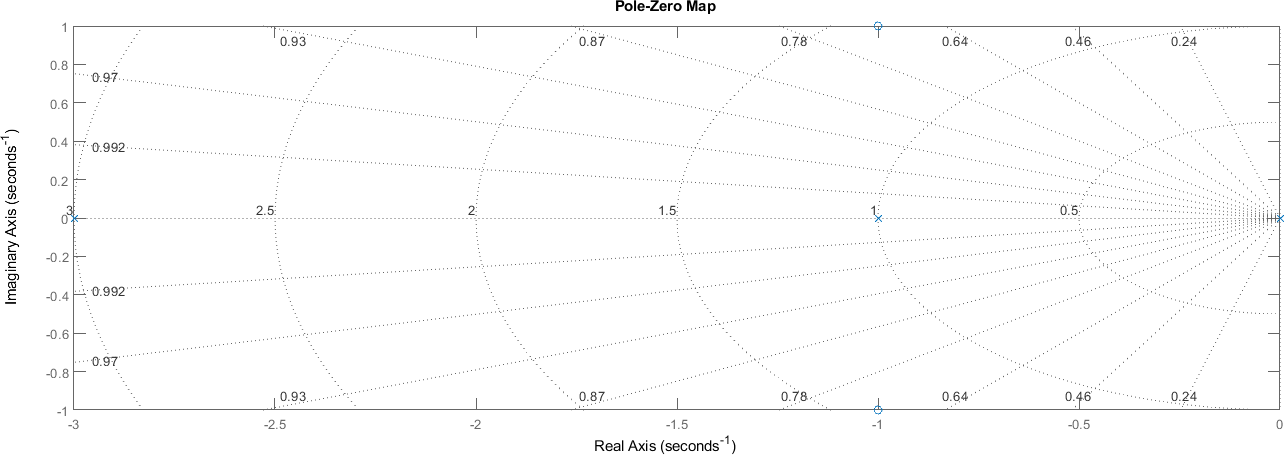
../_images/ELC05_Root_Locus_29_1.png

Para lograr el mismo gráfico en un modelo de Simulink, es necesario utilizar un bloque especial llamado Pole-Zero Plot

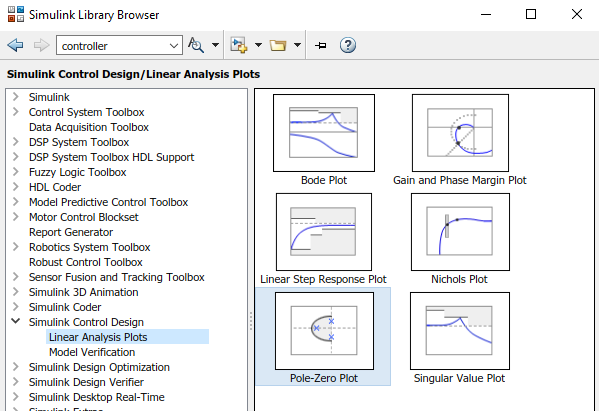
Este bloque puede ubicarse en cualquier parte del modelo ya que no es necesario conectarlo con las señales de manera directa

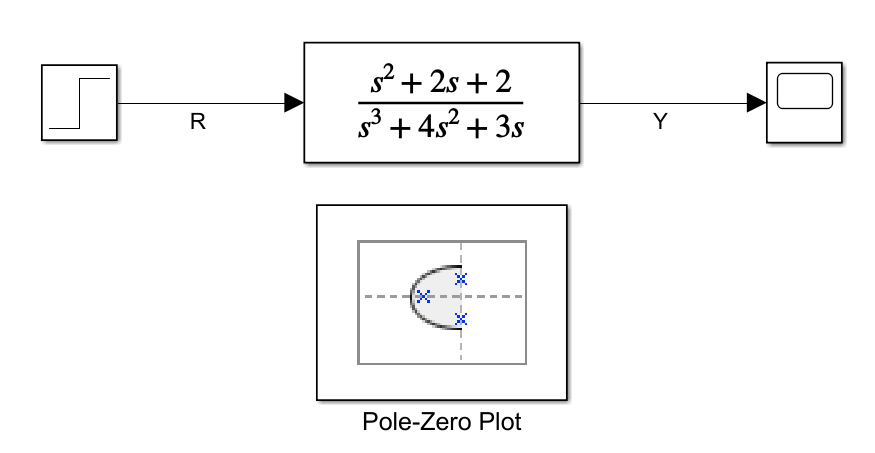
Luego, al abrirlo hay que explicitar cuál señal es la señal de entrada y cuál la de salida, esto se hace utilizando el botón +

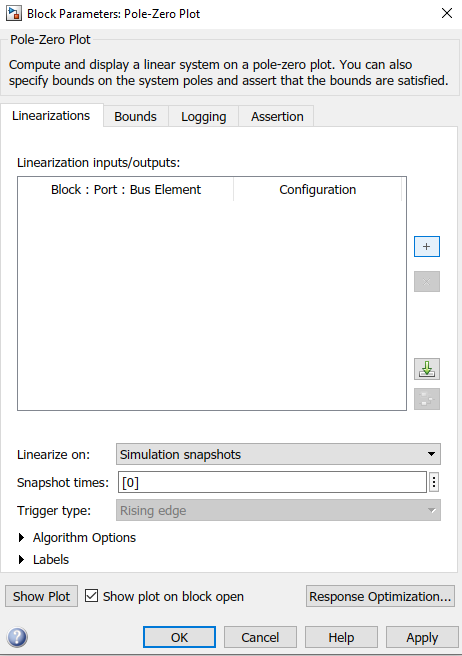
Al inicio el segundo panel estará vacio

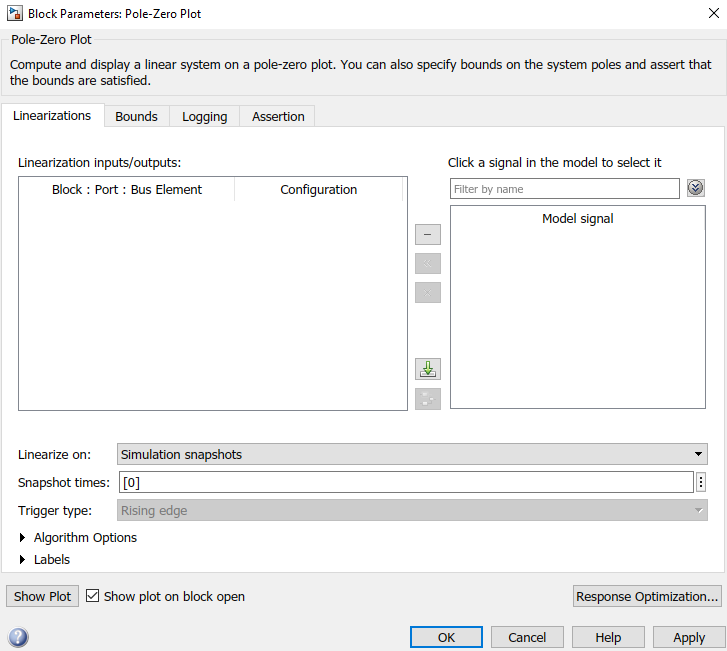
Para seleccionar una señal, basta con hacer click sobre ella en el modelo

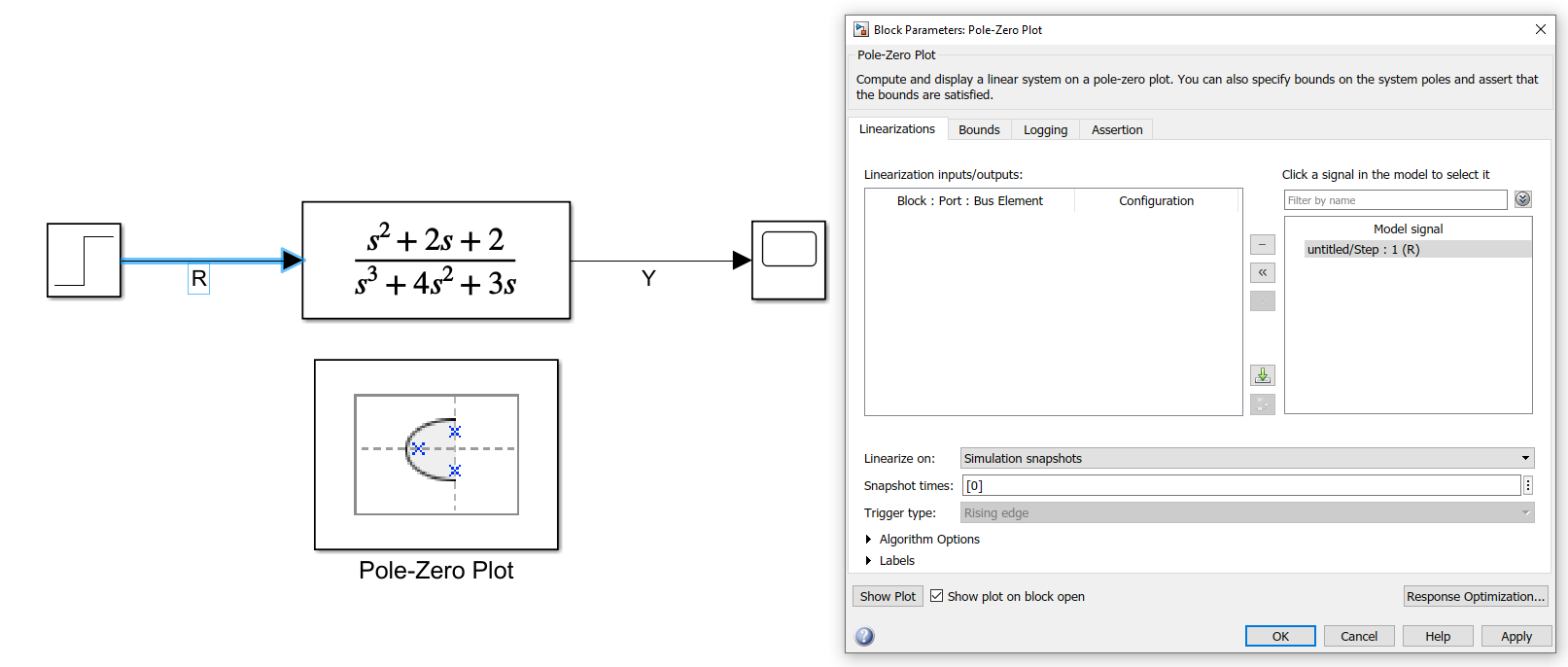
Y luego se presiona el botón << para agregar la señal al análisis

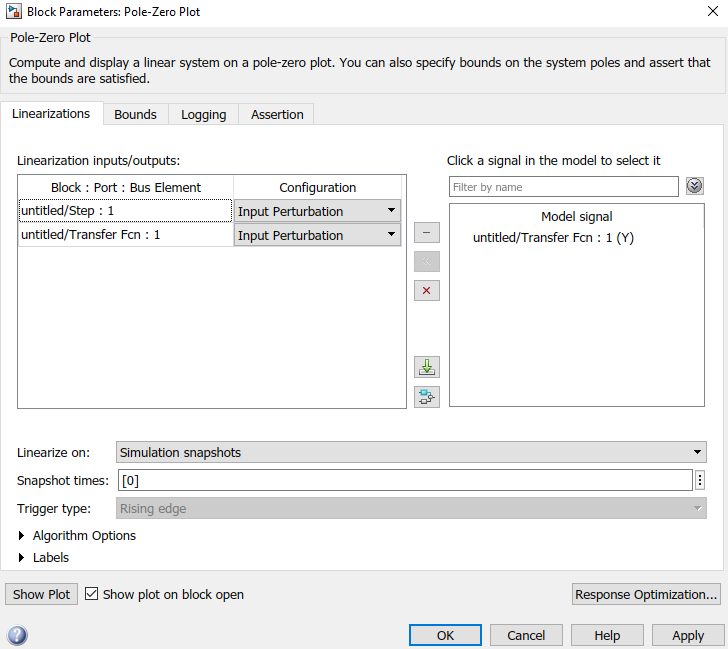
A continuación se debe configurar a la señal R como la entrada en lazo abierto y a la señal Y como la salida en lazo abierto

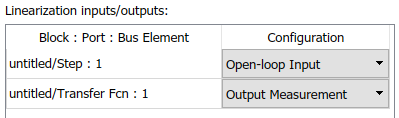
Finalmente se presiona Apply y se tilda la opción de Show plot on block open y se presiona Show Plot

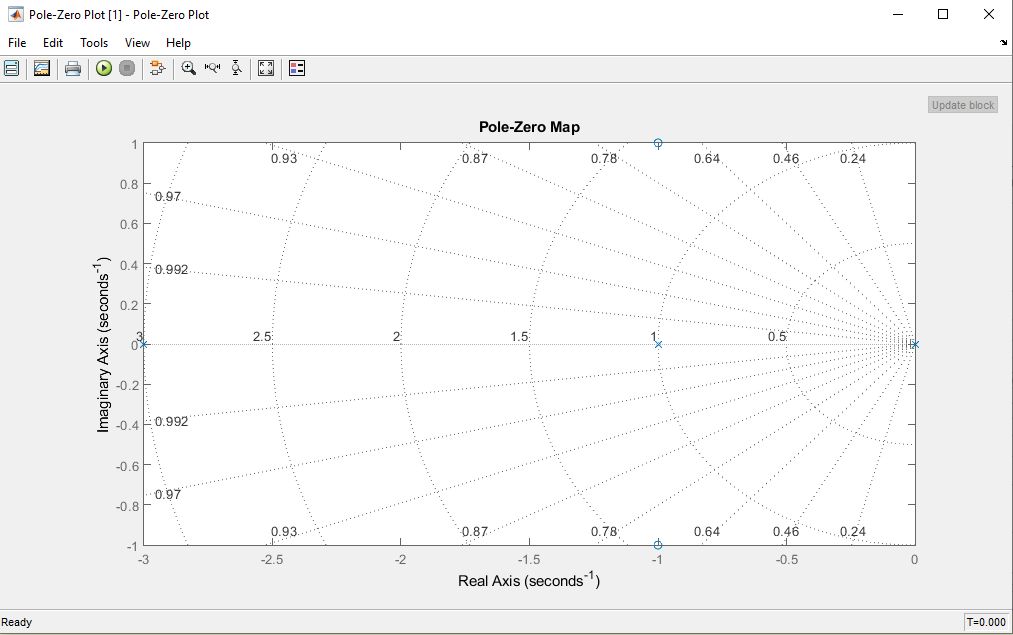
Al principio el gráfico estará vacio pero, luego de correr la simulación con el botón de play, se generará el gráfico adecuadamente.

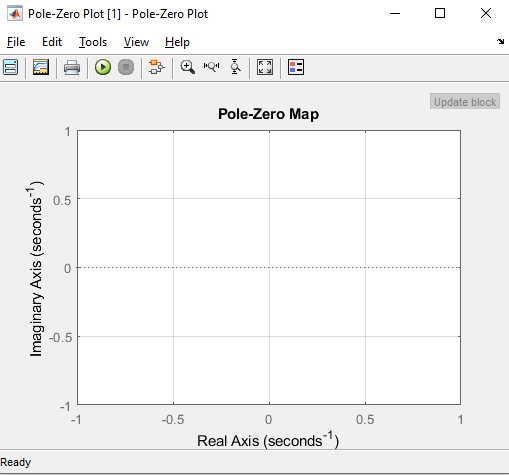
Se comprueba visualmente como los polos y ceros están en el mismo lugar que los obtenidos en el entorno de Matlab.

5.8. En Lazo Cerrado#

Al cerrar el lazo de retroalimentación, los polos y ceros cambian de posición

lazo_cerrado = feedback(sistema, 1)

lazo_cerrado =
 
      s^2 + 2 s + 2
  ---------------------
  s^3 + 5 s^2 + 5 s + 2
 
Continuous-time transfer function.

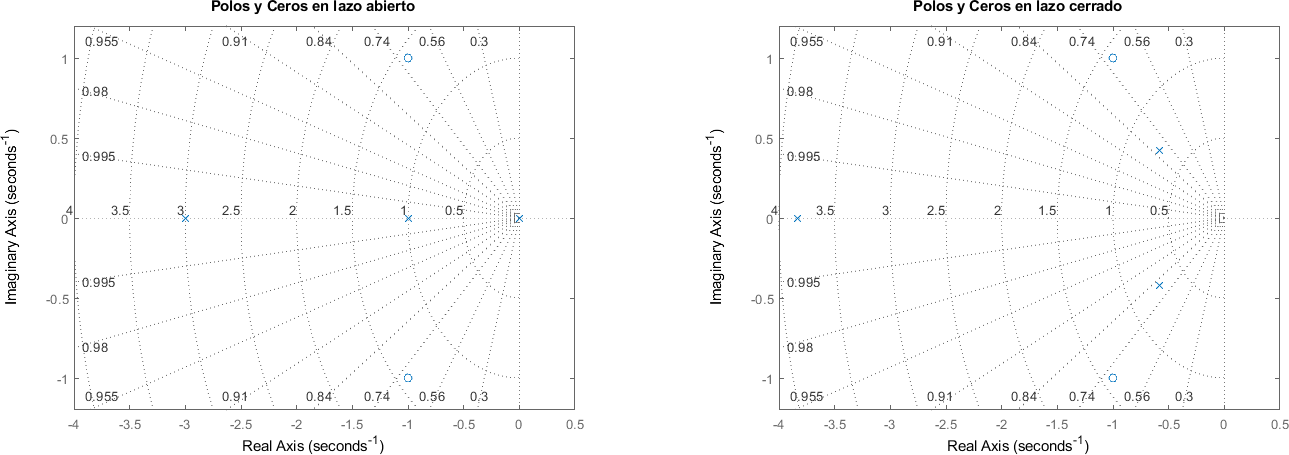
%plot inline --format=png -w 1600 -h 500

figure;
subplot(1, 2, 1)
pzmap(sistema)
xlim([-4 0.5])
ylim([-1.2 1.2])
title("Polos y Ceros en lazo abierto")
grid on

subplot(1, 2, 2)
pzmap(lazo_cerrado)
xlim([-4 0.5])
ylim([-1.2 1.2])
title("Polos y Ceros en lazo cerrado")

grid on
../_images/ELC05_Root_Locus_35_1.png

5.9. Diseño interactivo de Root Locus con Matlab#

Entender como leer un root locus es importante, pero también lo es saber que efectos tiene la adición / remoción de polos y ceros en un root locus determinado. Si bien las plantas no suelen ser modificables para agregar polos y ceros, los controladores sirven justamente para esto, permiten la incorporación de polos y ceros en lugares específicos. Para lograr esto se usa una aplicación especial dentro de Matlab llamada Control System Designer que requiere tener el Control System Toolbox instalado.

5.10. Control System Designer#

Para abrirla se debe ir a Apps > Control System Designer

Una vez abierta se deplegará una ventana similar a la siguiente

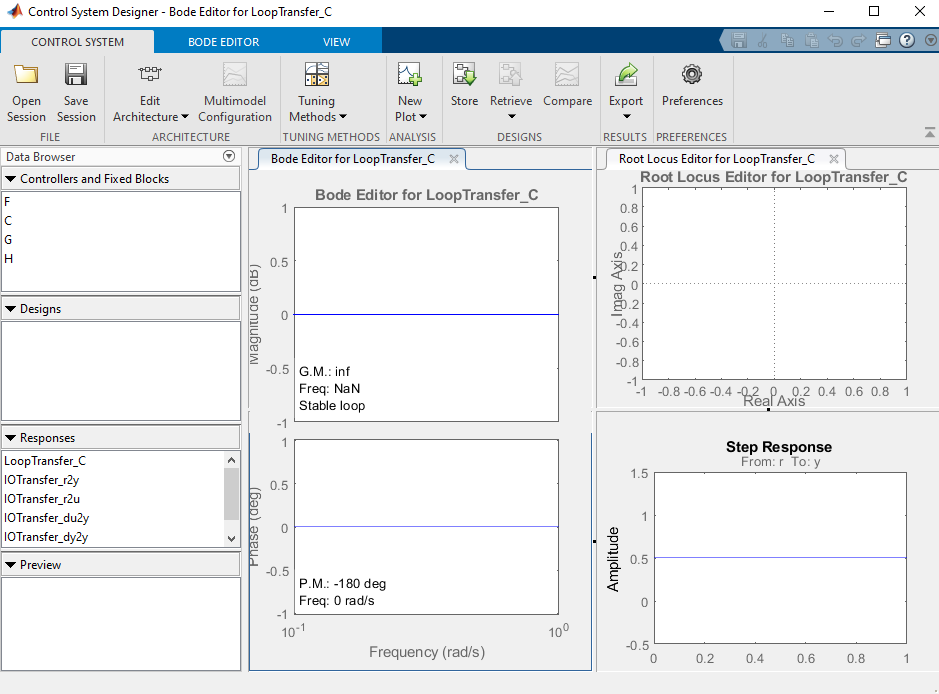
Se deben cerrar todos los gráficos para empezar la configuración de cero

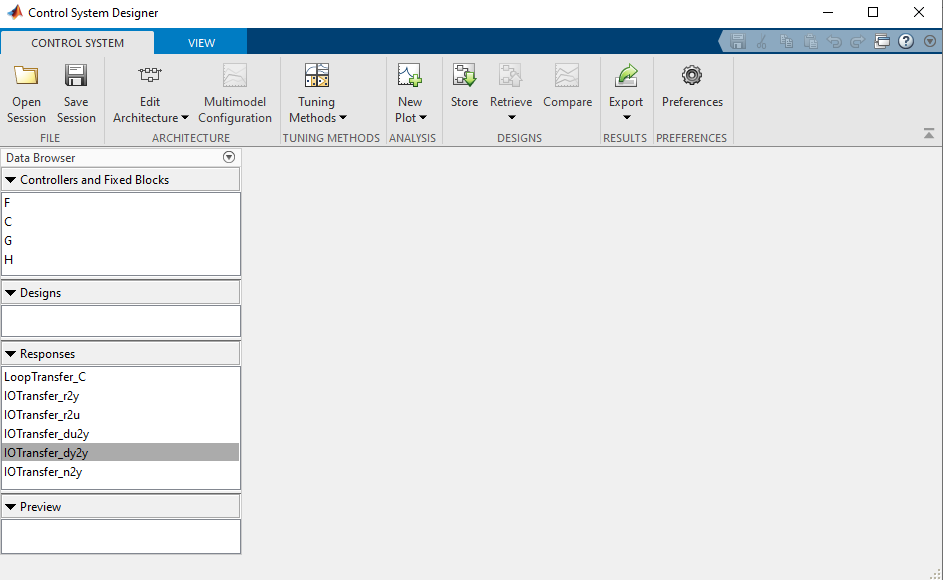
5.11. Seleccionar la arquitectura de control#

El primer paso es entender la arquitectura de control que se va a utilizar, para ello se debe presionar Edit Architecture

La arquitectura por defecto es la siguiente

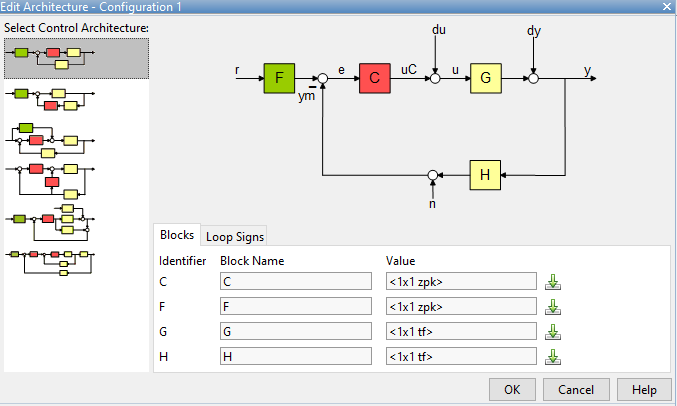
Donde G es la planta, H es el sensor, C es el controlador y F es la ganancia inicial. También se explicitan tres tipos de perturbaciones du, dy y n así como el error e, la entrada r y la salida y. Es posible darle valores a los bloques, aunque se asume que el único bloque modificable es C. En este notebook sólo se verán los temas referidos al root locus y no al diseño de controladores por lo que todos los valores se pueden dejar por defecto. Se debe presionar OK para cerrar la ventana.

5.12. Agregar Root Locus#

Para agregar el root locus, se debe seleccionar el Root Locus Editor dentro del menú Tuning Methods se abrirá una ventana donde no hacen falta cambios, se debe precionar Plot para continuar

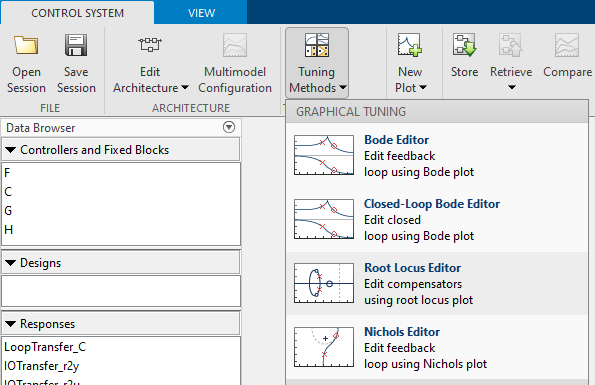
Luego el Root Locus debería aparecer en la ventana principal

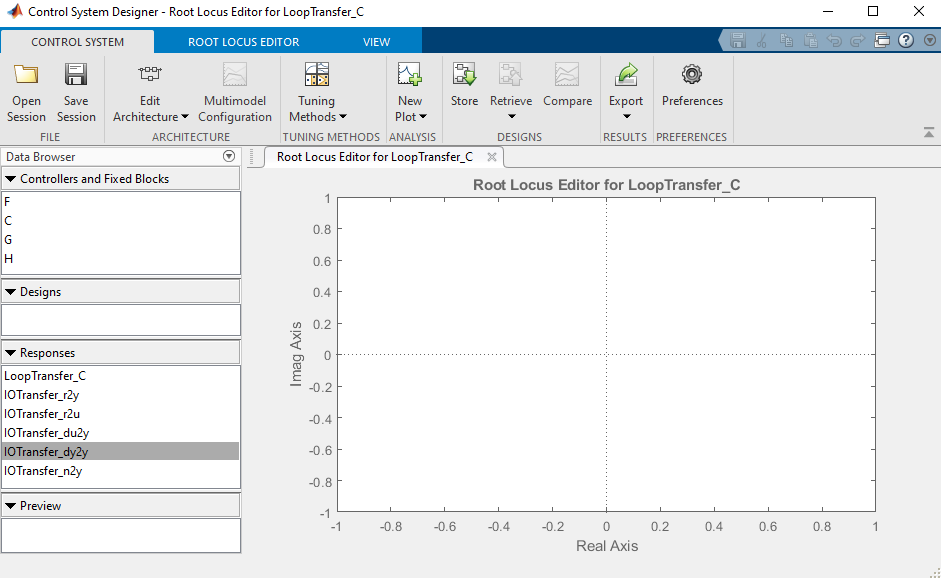
5.13. Agregar Respuesta en el tiempo y error#

5.13.1. Respuesta en el tiempo#

Otros dos gráficos relevantes son la salida en el tiempo ante una entrada escalón y el error en el tiempo ante una entrada del mismo tipo.

Para agregar estos gráfico se debe ir a New Plot y luego a New Step

Para la gráfica de la salida en función de la entrada es necesario aclarar que se quiere desde la señal R a la señal Y, luego se presiona Plot para agregar el gráfico. El gráfico debería aparecer en la ventana principal.

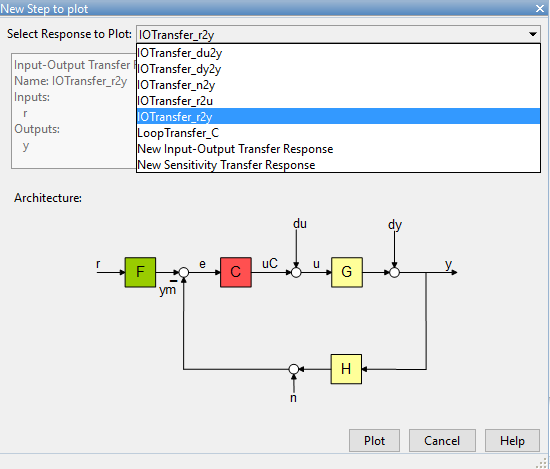
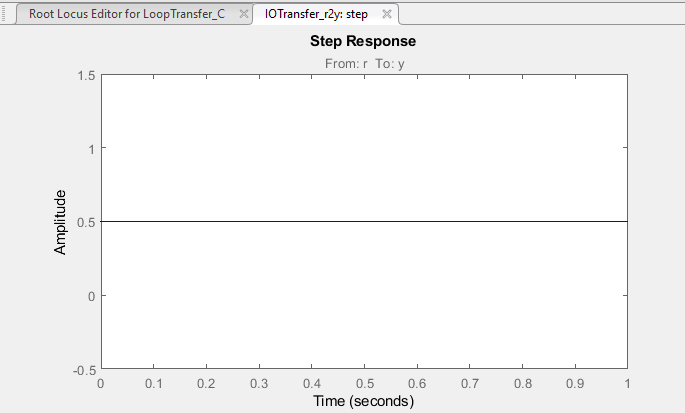
Como el sistema aún no tiene definido ni polos ni ceros, la entrada es un escalón unitario y la salida es un escalón unitario atenuado con amplitud de 0.5

5.13.2. Error en función del tiempo#

Para el caso del error los pasos son similares, pero no existe en el menú de New Step un gráfico asociado a r2e, que sería el error en función de la entrada. No obstante esta combinación puede agregarse seleccionando New Input-Output Transfer Response. Al seleccionarlo la pantalla cambiará, permitiéndo especificar señales de entrada y de salida.

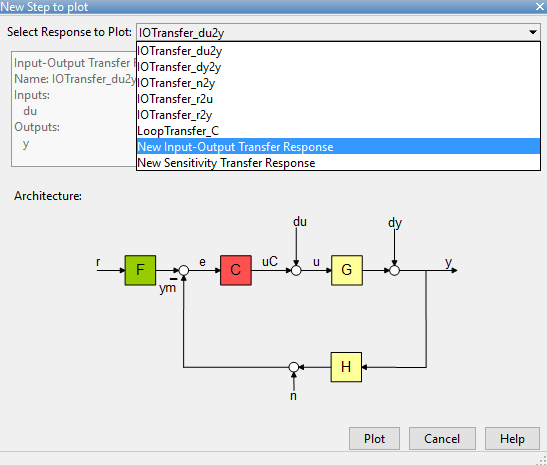
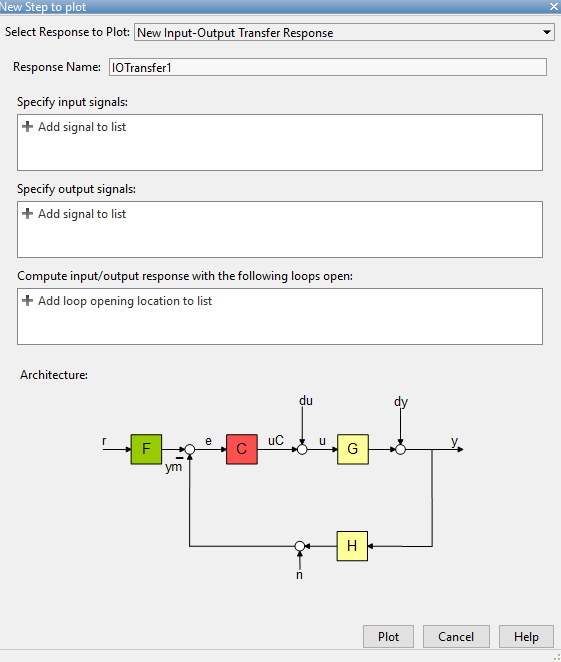
Se debe seleccionar r como entrada y e como salida y luego presionar Plot

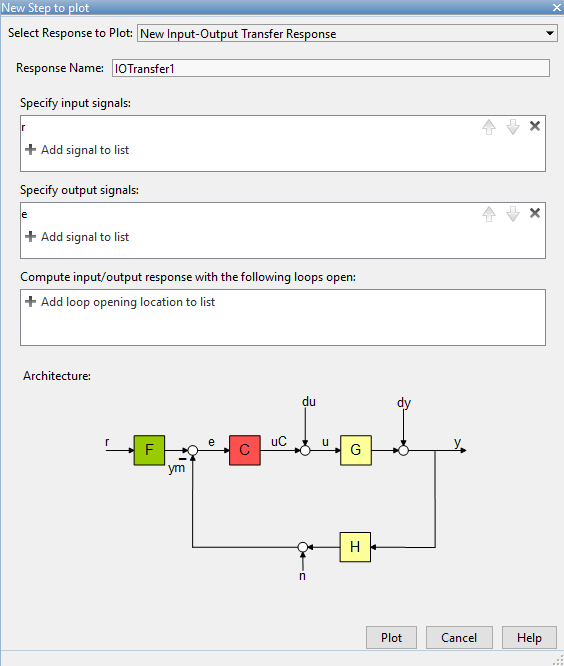
Se agregará otro gráfico a la ventana principal, que en este caso será igual al anterior ya que el error se mantiene constante en 0.5.

A continuación se acomodan las pestañas de los gráficos para poder mostrar tanto el root locus como ambas salidas al mismo tiempo. Para acomodar las vistas, basta con arrastrar y soltar.

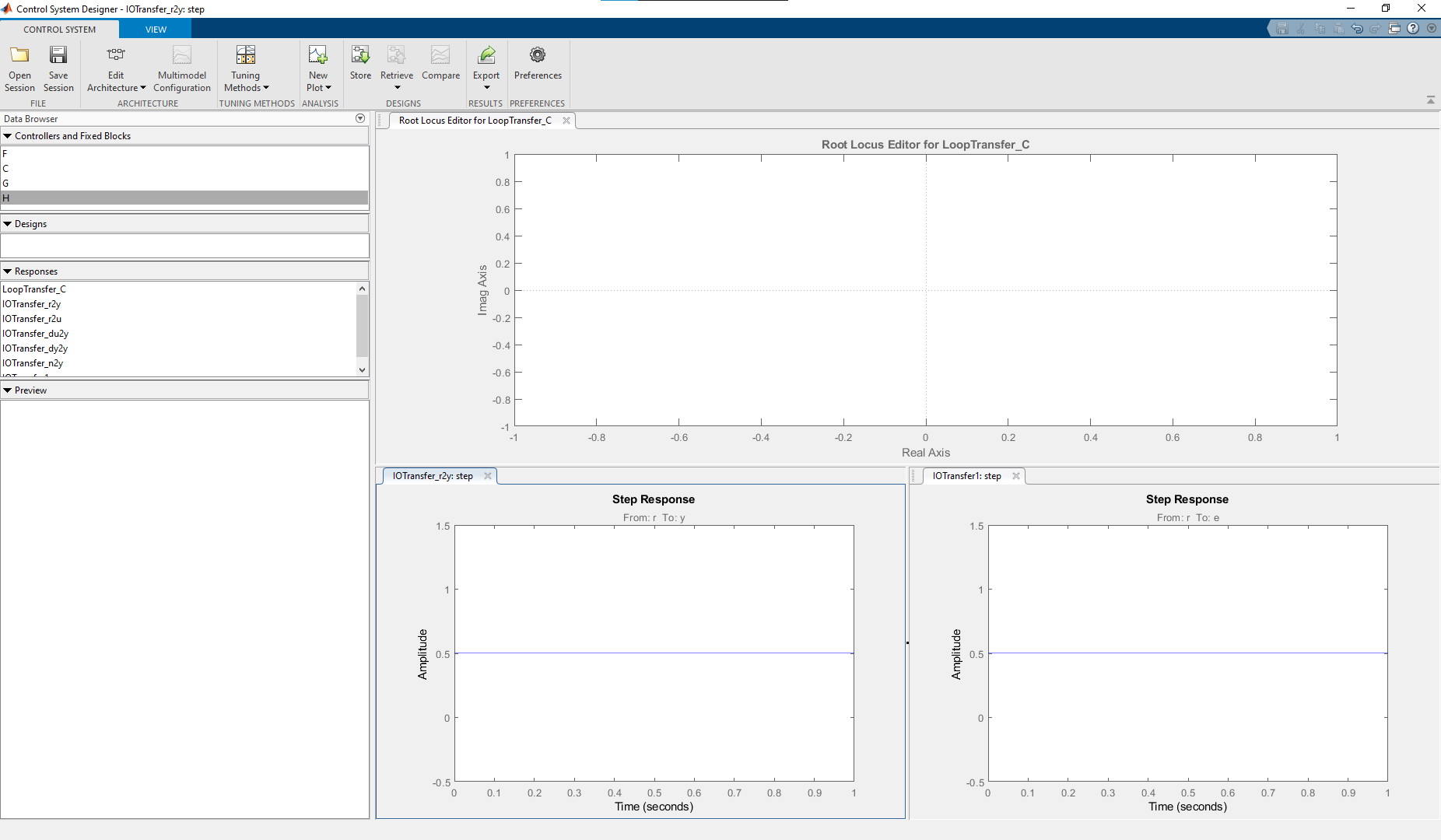
5.14. Editando el Root Locus Dinámicamente con la interfaz gráfica#

Ahora es posible modificar el root locus y ver como las salidas cambian. para ello basta con hacer click en el gráfico de root locus y luego ir a la pestaña de Root Locus Editor

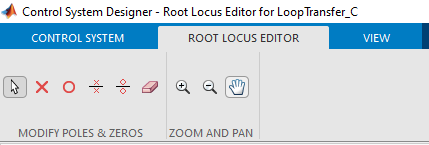
Utilizando los botones se pueden agregar polos y ceros reales, polos y ceros complejos y borrar los ya agregados.

También es posible hacerlo al ver el menú contextual que se despliega al hacer click derecho sobre el gráfico del root locus. En este caso se suman las opciones de agregar un controlador integral (Integrator), un controlador derivativo (Differentiator) y tres tipos de compensadores Lead, Lag y Notch.

  • El Integrador agrega un polo en el origen

  • El derivativo agrega un cero en el origen

  • El Lead agrega un polo y un cero, con el cero más cerca del origen que el polo

  • El Lag agrega un polo y un cero, con el polo más cerca del origen que el cero

  • El Notch agrega dos polos complejos y dos ceros complejos, con los ceros más cerca del origen que los polos

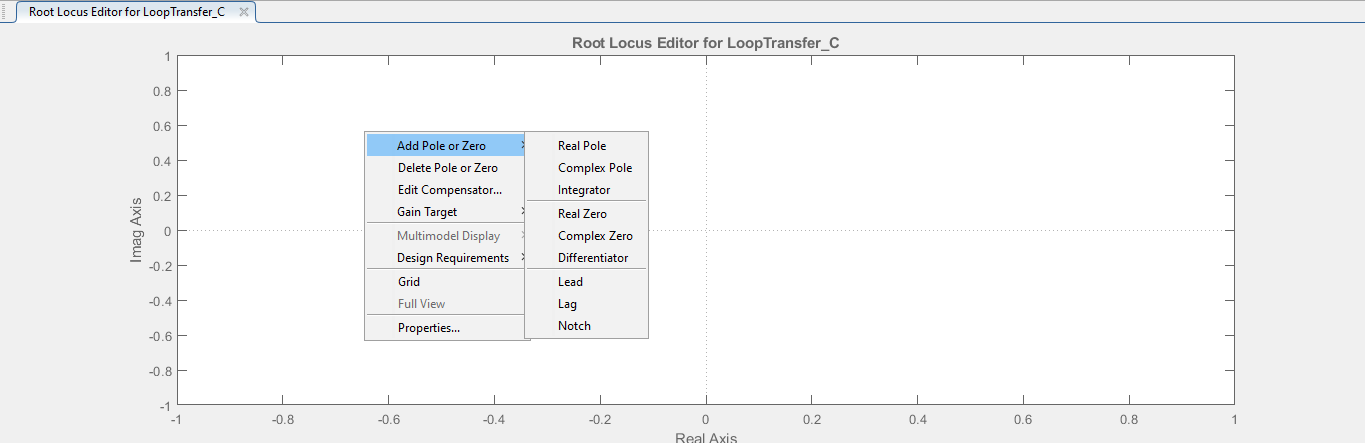
Un ejemplo de sistema podría ser

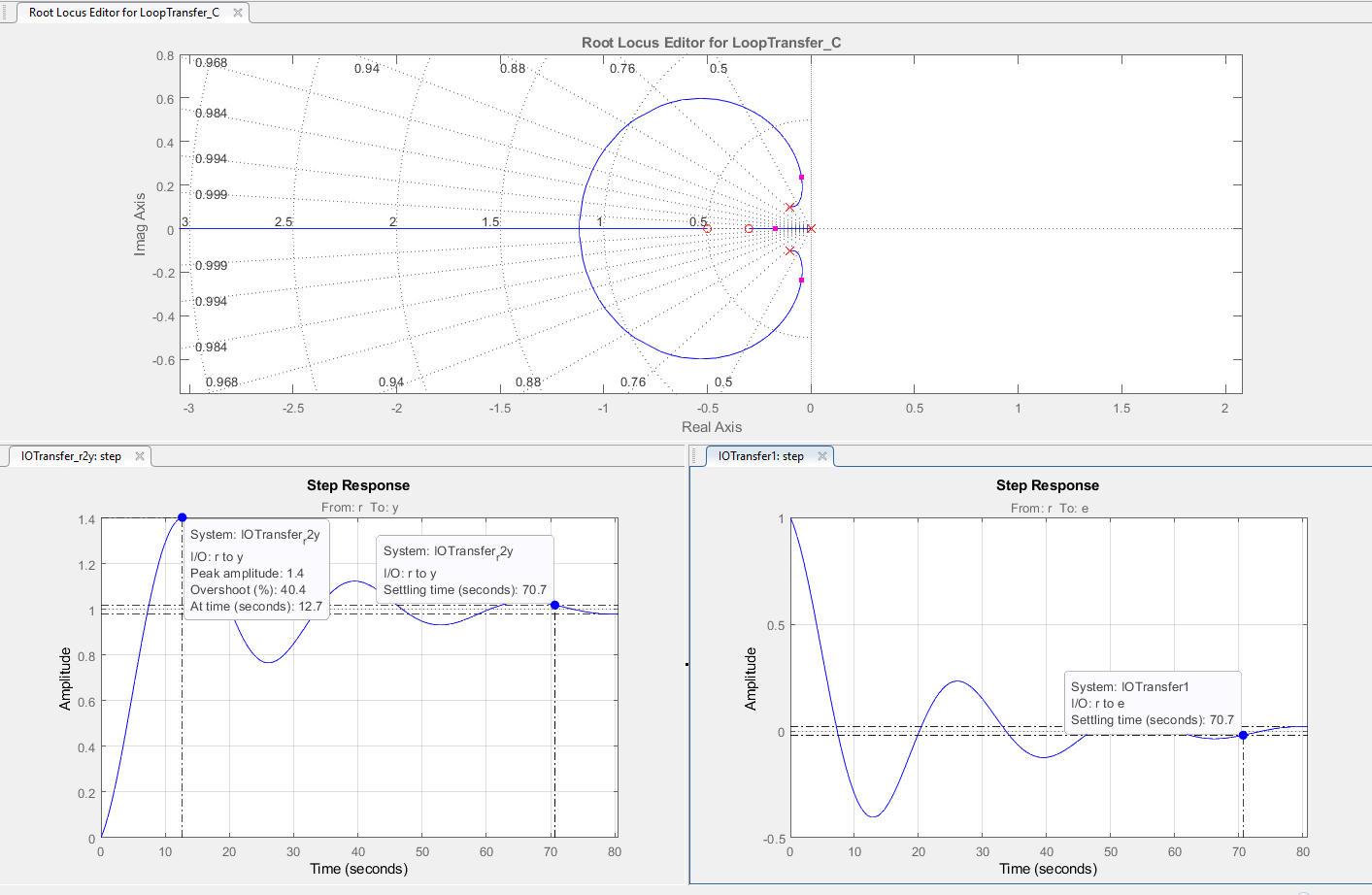
Que emula a una planta de segundo orden con dos polos complejos con un controlador PID.

La parte más importante de esta herramienta es que todos los polos y ceros agregados (cruces y cículos) así como las ganancias (cuadrados púrpuras) pueden arrastrarse y soltarse en los diferentes puntos del root locus, y es posible ver como la forma del root locus y las salidas en el tiempo cambian al hacerlo. Además, pueden verse las características de las gráficas con forme se modifica el root locus

5.15. Editando el Root Locus Dinámicamente con el editor de compensador#

Otra manera de editar el root locus es ingresar los valores exactos directamente, para ello, se debe hacer click derecho en el Root Locus y luego en “Edit Compensator...”

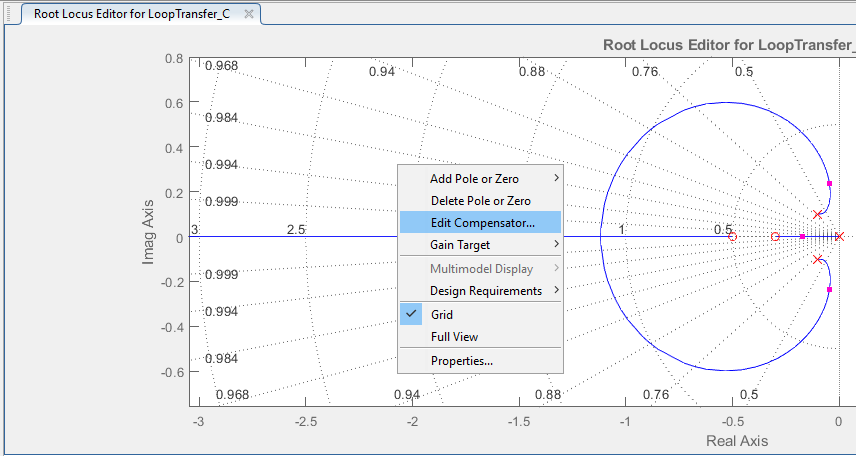
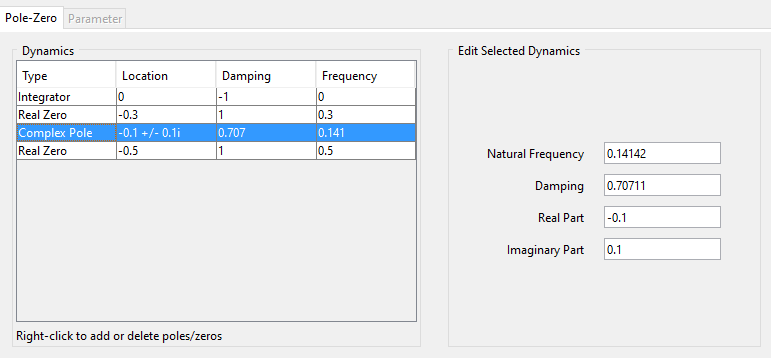
Esta opción abre una nueva ventana donde uno puede editar los valores de cada polo y cero y también agregar nuevos o borrar los actuales haciendo click derecho. Las opciones para agregar polos y ceros son las mismas que en la gráfica del Root Locus

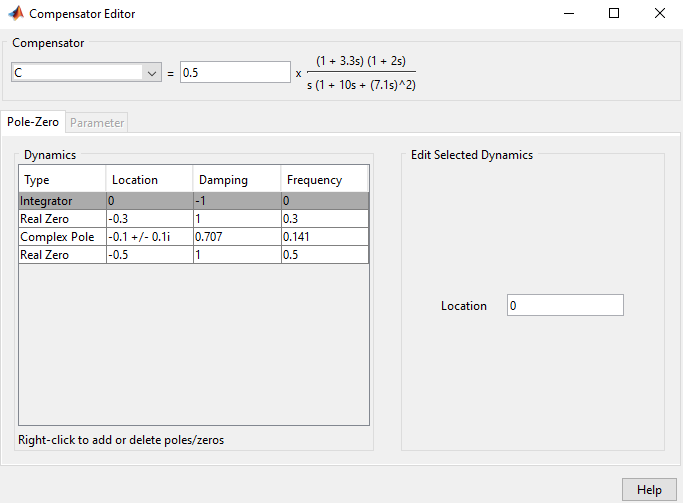
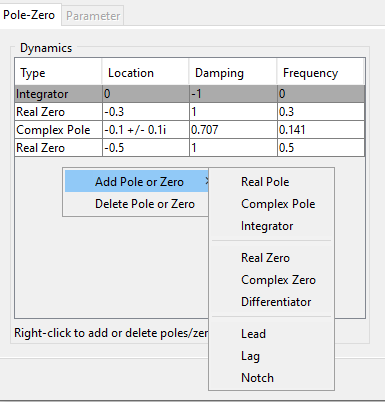
Algunas características interesantes de esta vista de editor son:

  • Se puede ver el valor de la ganancia y la forma de la función de transferencia asociada al root locus mostrado:

  • En el caso de los polos y ceros complejos se pueden especificar de manera rectangular (con parte real e imaginaria) o de manera polar (con frecuencia natural y coeficiente de amortiguamiento)

5.16. Referencias y Recursos Útiles#