8. Diagramas de Bode#

Version 0.1

Contenido Original creado por Ezequiel Leonardo Castaño

Este contenido está INCOMPLETO y puede estar incompleto y/o sufrir modificaciones

Material faltante en este capítulo:

  • Como interpretar un diagrama de Bode en sistemas de fase no mínima

  • Diagrama de Bode para un polo o cero complejo

  • Diagrama de Bode en Simulink

  • Sintonización basada en diagrama de Bode en Simulink

%plot inline --format=png -w 1600 -h 800

format compact;

8.1. Fase Mínima y Fase no Mínima#

Un sistema es de face mínima si y sólo si todos sus polos y ceros en lazo abierto están a la izquierda del eje imaginario. Esto no debe confundirse con la estabilidad del sistema ya que la estabilidad del sistema está dada únicamente por los polos y no por los ceros.

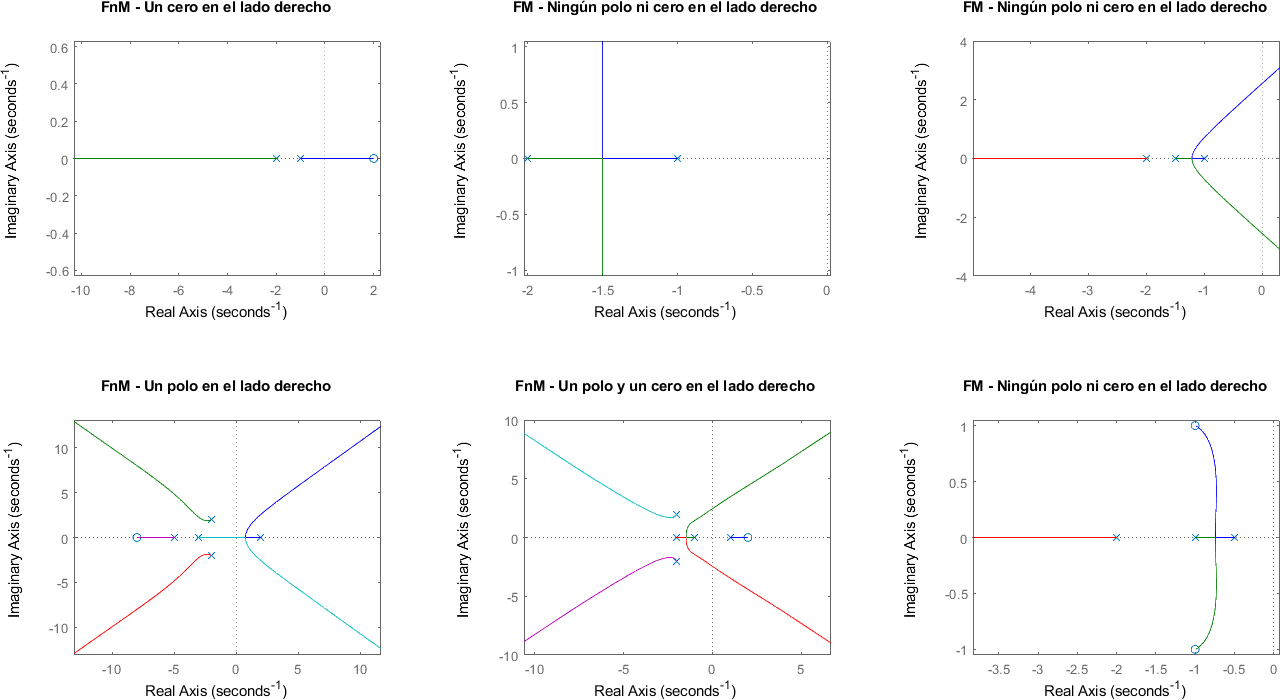
A continuación se muestran algunos ejemplos para diferenciar entre Fase Mínima (FM) y Fase no Mínima (FnM). Todos los ejemplos son con funciones de transferencia en lazo abierto.

figure;

subplot(2, 3, 1)
sistema = zpk(2, [-1 -2], 1);
rlocus(sistema)
title("FnM - Un cero en el lado derecho")

subplot(2, 3, 2)
sistema = zpk([], [-1 -2], 1);
rlocus(sistema)
title("FM - Ningún polo ni cero en el lado derecho")

subplot(2, 3, 3)
sistema = zpk([], [-1 -2 -1.5], 1);
rlocus(sistema)
title("FM - Ningún polo ni cero en el lado derecho")

subplot(2, 3, 4)
sistema = zpk(-8, [2 -5 -3 -2+2j -2-2j], 1);
rlocus(sistema)
title("FnM - Un polo en el lado derecho")

subplot(2, 3, 5)
sistema = zpk(2, [1 -1 -2 -2+2j -2-2j], 1);
rlocus(sistema)
title("FnM - Un polo y un cero en el lado derecho")

subplot(2, 3, 6)
sistema = zpk([-1+1i; -1-1i], [-1 -2 -0.5], 1);
rlocus(sistema)
title("FM - Ningún polo ni cero en el lado derecho")
../_images/ELC08_Bode_4_1.png

8.2. Diagrama de Bode#

El diagrama de Bode sólo se puede aplicar en sistemas de fase mínima

Es importante recordar que en el caso de sistemas SISO LTI, al someter a un sistema a una entrada senoidal, la salida en estado estable será también una señal senoidal con la misma frecuencia, sin embargo puede haber un cambio de amplitud y/o un cambio de fase.

Para construir un diagrama o traza de Bode se deben seguir los siguientes pasos:

  1. Someter el sistema a una entrada senoidal con una determinada frecuencia \(\omega\) y una amplitud \(A\)y esperar a llegar al estado estable

  2. Variar \(\omega\) desde \(0\) hasta \(+\infty\)

  3. Generar un gráfico que muestre la relación entre la amplitud de salida \(A^{\prime }\) y la de entrada \(A\) para cada valor de \(\omega\), este gráfico es el gráfico de Magnitud-Frecuencia. En este gráfico la amplificación o atenuación de la amplitud se suele expresar en \(dB\)

  4. Generar un gráfico que muestre la relación entre la la fase de entrada \(0º\) y la de salida, este gráfico es el gráfico de Fase-Frecuencia.

  5. Un detalle en la construcción es que tanto la Magnitud como la Frecuencia se encuentran en escala logarítmica, la magnitud por estar expresada en \(dB\) y la frecuencia para poder cubrir un amplio espectro de posibilidades.

8.3. Desarrollo matemático#

Al utilizar la transformada de Laplace, la variable a utilizar, \(s\), es una variable compleja, es decir:

\[s=\sigma +\omega i~~\sigma ,\omega \in \mathbb{R}\]

Pero, como el diagrama de Bode considera el sistema en estado estable, \(\sigma\) puede considerarse nula, ya que en toda solución estable de sistemas LTI SISO se cumple

\[\lim_{s\to \infty } \sigma =0\]

Es por ello que al analizar una función de transferencia, si sólo se considera el estado estable se tiene que:

\[G(s)=G(\sigma +\omega i)\Rightarrow G(s)=G(\omega i)\]

Utilizando esta forma se procede a calcular tanto la magnitud como la fase

8.4. Entrada#

Dada una entrada senoida

\[u(t)=A\cdot sen(\omega t)\]

Por las propiedades del sistema LTI, la salida va a ser de la forma

\[y(t)=B\cdot sen(\omega t+\phi )\]

Al aplicar la transformada de Laplace se tiene una entrada \(U(s)\)

\[U(s)=\frac{A\cdot \omega }{s^2 +\omega^2 }\]

Y al transformar la salida se tiene una salida \(Y(s)\)

\[Y(s)=\frac{B\cdot (\omega \cdot cos(\phi )+s\cdot sin(\phi ))}{s^2 +\omega^2 }\]

Para demostrar esto se debe partir de una función de salida expresada en función de la entrada por una función de transferencia

\[Y(s)=G(s)\cdot U(s)\]

Si se expresa \(G(s)\) de manera genérica y \(U(s)\) como está arriba se tiene

\[Y(s) = k\cdot \frac{(s+z_1 )(s+z_2 )...(s+z_m )}{(s+p_1 )(s+p_2 )...(s+p_n )}\cdot \frac{A\cdot \omega }{s^2 +\omega^2 }\]

Al hacer descomposición en fracciones parciales se tiene

\[Y(s)=\frac{C_1 }{s+p_1 }+\frac{C_2 }{s+p_2 }+...+\frac{C_n }{s+p_n }+\frac{C_e }{s+i\omega }+\frac{C_f }{s-i\omega }\]

Luego al aplicar la antitransformada se tiene

\[y(t)=C_1 \cdot e^{-p_1 t} +C_2 \cdot e^{-p_2 t} +...+C_n \cdot e^{-p_n t} +C_e \cdot e^{-i\omega t} +C_f \cdot e^{i\omega t}\]

Sin embargo, al evaluar únicamente el estado estacionario, se puede asumir que el valor de t es suficientemente o tiende asintóticamente a \(\infty\). Quedando de esta forma:

\[\lim_{t\to \infty } y(t) = B\cdot sin(\omega t+\phi )\]

Se llega entonces a que la respuesta en el tiempo una vez alcanzado el estado estacionario tendrá la forma

\[y(t)=B\cdot sin(\omega t+\phi )\]

Ahora sólo resta determinar el valor de \(B\) y de \(\phi\), que son los parámetros que definen a la salida del sistema. Donde \(\phi\) es el ángulo de entre el eje real y el punto en el plano complejo \(Y(s)\)y se lo conoce como fase, mientras que \(B\) es la amplitud de la salida y se calcula de la siguiente forma

\[B=A\cdot |G(i\omega )|\]

Donde \(|G(i\omega )|\) es la magnitud y \(A\) es la amplitud de la entrada. Lo que interesa en realidad no es el valor exacto de \(B\), sino la relación de amplitudes es decir, cuanto la amplitud de salida fue amplificada o atenuada. Esta relación de amplitud es el cociente entre la amplitud de salida y la de entrada, es decir:

\[\frac{B}{A}=\frac{A\cdot |G(i\omega )|}{A}=|G(i\omega )|\]

Por lo tanto la magnitud de la función de transferencia refleja cual es la relación entre la amplitud de entrada y la de salida

A continuación se muestra como calcular ambas cantidades.

8.4.1. Magnitud#

Como la función \(G(i\omega )\)puede expresarse como un cociente de polinomios se tiene:

\[Magnitud(G)=|G(i\omega )|=\Bigl|\;k\cdot \frac{(i\omega +z_1 )(i\omega +z_2 )...(i\omega +z_m )}{(i\omega +p_1 )(i\omega +p_2 )...(i\omega +p_n )}\Bigr|\]

Aplicando propiedades de los módulos, se obtiene

\[Magnitud(G)=k\cdot \frac{|(i\omega +z_1 )(i\omega +z_2 )...(i\omega +z_m )|}{|(i\omega +p_1 )(i\omega +p_2 )...(i\omega +p_n )|}\]

Para calculos los módulos del numerador y del denominador, se usa la representación rectangular de los números complejos, en esta forma, se define a la magnitud como la distancia euclideana en el plano complejo del origen al punto asociado a un \(\omega\) específico. Esta distancia puede calcularse por teorema de pitágoras como:

\[Magnitud(G)=\sqrt{real^2 +imaginario^2 }\]

Esto quiere decir que el primer paso es trabajar algebraicamente el numerador y el denominador para llevarlos a la forma binómica, para ello todos los términos con la unidad imaginaria \(i\) deben agruparse y luego podrá expresarse la magnitud como

\[Magnitud(G)=k\cdot \frac{\sqrt{real\_numerador^2 +imaginario\_numerador^2 }}{\sqrt{real\_denominador^2 +imaginario\_denominador^2 }}\]

Adicionalmente, la magnitud suele expresar en decibelios que es una unidad logarítmica definida de la siguiente forma

\[Magnitud_{dB} (G)=20\log_{10} \Big(\frac{B}{A}\Big)=20\log_{10} \Big(\frac{A\cdot |G(i\omega )|}{A}\Big)=20\log_{10} (|G(i\omega )|)\]

De ahora en más, como siempre se usará la magnitud expresada en decibelios, se omite el súbindice \(dB\)**.

8.5. Fase#

En el caso de la fase, no hay una fórmula que pueda expresarse en función del numerador y el denominador sino que se tiene que llevar a expresión a la forma binómica y utilizar la tangente de la representación rectangular para hallar el ángulo \(\phi\). Es decir

\[Fase(G)=~\phi = \tan^{-1} \Bigl(\frac{imaginario}{real}\Bigr)\]

8.6. Construcción del diagrama de Bode#

8.7. Construcción aditiva#

Una de las ventajas del diagrama de Bode es que su construcción es aditiva, es decir, el diagrama asociado a una función de transferencia es igual a la suma de los diagramas de sus ceros y polos.

Esto puede demostrarse de la siguiente forma

\[\begin{array}{cllr} G(i\omega )= k\cdot (i\omega +z_1 )\cdot (i\omega +z_2 )~...~(i\omega +z_m )\cdot \frac{1}{(i\omega +p_1 )}\cdot \frac{1}{(i\omega +p_2 )}~...~\frac{1}{(i\omega +p_n )} \end{array}\]

Entonces al calcular la magnitud

\[Magnitud(G) = 20\cdot \Big\lbrack \log_{10} (|k|)+\log_{10} (|i\omega +z_1 |)+\log_{10} (|i\omega +z_2 |)+...+\log_{10} (|i\omega +z_m |)-\log_{10} (|i\omega +p_1 |)-\log_{10} (|i\omega +p_2 |)-...-\log_{10} (|i\omega +p_n |)\Big\rbrack\]

Para la Fase el proceso es similar y se basa en el teorema del argumento del producto de números complejos. La desmostración es un poco más extensa así que se deja \href{https://proofwiki.org/wiki/Argument_of_Product_equals_Sum_of_Arguments}{un recurso} donde se detalla paso a paso para el lector interesado. La conclusión del teorema es

\[Fase(G)=\phi =Fase(G(i\omega ))=Fase(k)+Fase(i\omega +z_1 )+Fase(i\omega +z_2 )+...+Fase(i\omega +z_m )+Fase\Big(\frac{1}{i\omega +p_1 }\Big)+Fase\Big(\frac{1}{i\omega +p_2 }\Big)+...+Fase\Big(\frac{1}{i\omega +p_n }\Big)\]

En las expresiónes anteriores puede verse como en lugar de calcular la magnitud y la fase para una función de transferencia \(G(i\omega )\) genérica, se pueden sumar los componentes representados por sus polos, ceros y la ganancia.

A continuación se muestran los bloques fundamentales que permiten graficar cualquier función de transferencia usando el método aditivo. Para ello hace falta conocer cúal es la magnitud y fase de:

  • Una Ganancia

  • Un Polo/Cero en el Origen

  • Un Polo/Cero Real

  • Un Polo/Cero Complejo

Conociendo como se esboza un diagrama de Bode para todos estos casos, se puede graficar cualquier función de transferencia.

8.8. Sistema Constante#

Un sistema constante es aquel definido por

\[G(s)=K~~K\in \mathbb{R}\]

Esta constante es normalmente llamada ganancia y el diagrama de bloques equivalente es

8.8.1. Definiendo el sistema#

Se definen dos sistemas, uno con ganancia positiva \(K=10\) y otro con ganancia negativa \(K=-10\). También se explicita el rango de frecuencias a utilizar

sistemas = {};
sistemas{1} = zpk([], [], 10);
sistemas{2} = zpk([], [], -10);

frecuencia = logspace(-1, 3, 1000);

8.8.2. Magnitud#

Utilizando las fórmulas de la introducción se tiene entonces:

\[Magnitud(G)=20\cdot \log_{10} (|G(i\omega )|)=20\cdot \log_{10} (|K|)\]

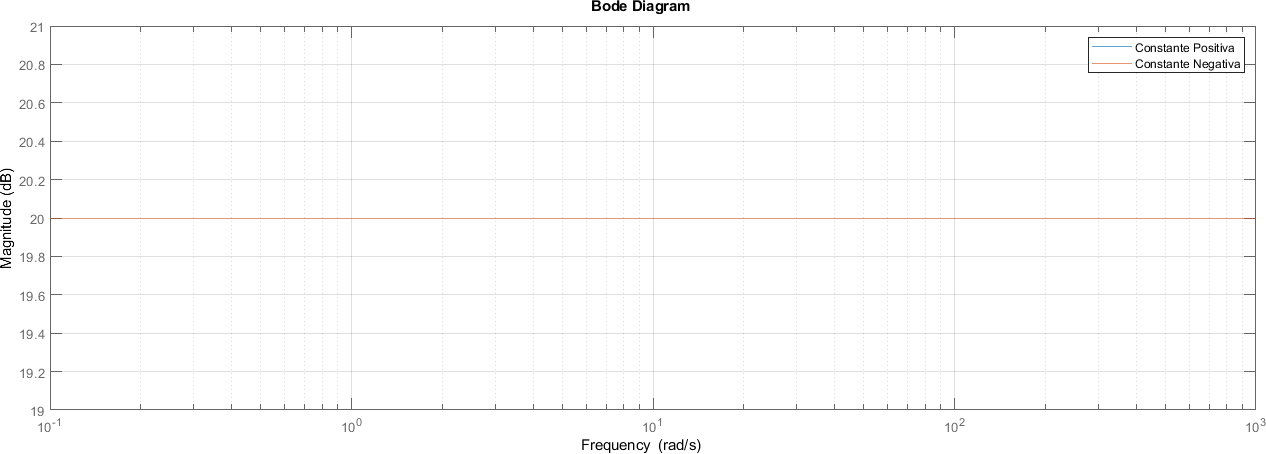
Como la magnitud no tiene ningún \(\omega\), el valor de la magnitud será constante para todo el espectro de frecuencias.

Concretamente, para los valores de \(k\in \lbrace -10,10\rbrace\), el valor de la magnitud será de \(20dB\)

En este caso ambas gráficas se ven superpuestas en el mismo valor

%plot inline --format=png -w 1600 -h 500

figure;
hold all

bodemag(sistemas{:}, frecuencia)

legend("Constante Positiva", "Constante Negativa")
grid on
../_images/ELC08_Bode_20_1.png

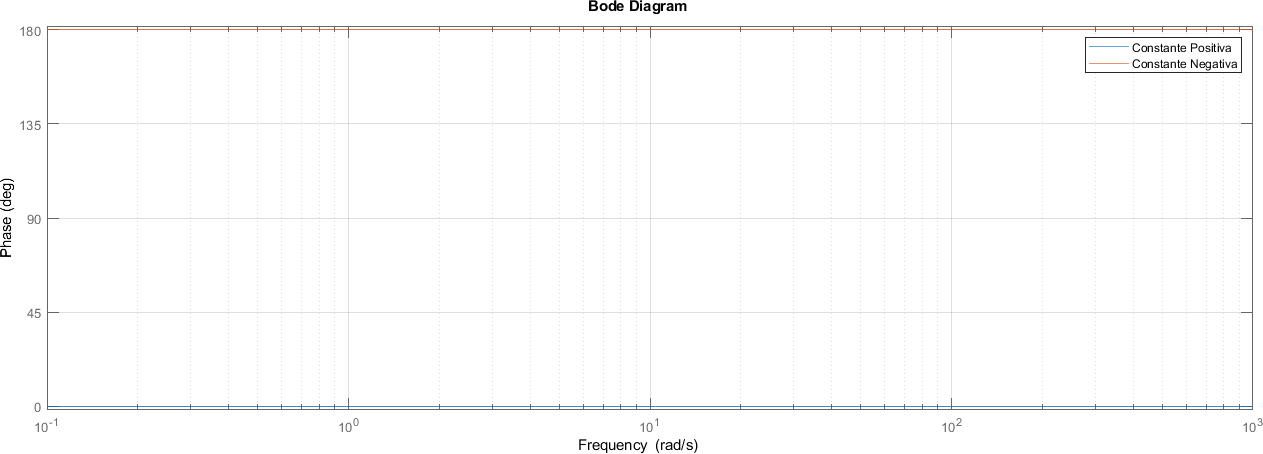
8.8.3. Fase#

Para el cálculo de la fase se tiene

\[Fase(G)=~\phi =\tan^{-1} \Bigl(\frac{imaginario}{real}\Bigr)\]

Entonces:

\[\tan^{-1} \Bigl(\,\frac{0}{K}\,\Bigr)=\left\lbrace \begin{array}{cc} \pi & ~~\textrm{if}\;K<0 \end{array}\right.\]

Esto quiere decir que la fase será constante y que podrá tener un valor de \(0º\) o de \(180ª\) (\(\pi\) radiantes). Entonces la fase depende de manera exclusiva del **signo} de \(K\) y no de su valor absoluto.

figure;
hold all

h = bodeplot(sistemas{:}, frecuencia);
setoptions(h, 'MagVisible', 'off');

legend("Constante Positiva", "Constante Negativa")
grid on
../_images/ELC08_Bode_22_1.png

8.9. Sistema con un Polo o un Cero en el origen#

Un sistema con un polo en el origen puede describirse como

\[G(s)=\frac{1}{s}\]

Si se reemplaza \(s\) con \(i\omega\) se tiene entonces:

\[G(i\omega )=\frac{1}{i\omega }=\frac{1}{i\omega }\cdot \frac{i}{i}=\frac{i}{-\omega }=-\frac{1}{\omega }i\]

La representación en diagrama de bloques es

8.9.1. Cero en el origen#

Una función de transferencia con un cero en el origen está definida como

\[H(s)=s\]

La representación en diagrama de bloques es

Sin embargo, herramientas como Simulink no permiten crear funciones de transferencia impropias, por lo que se suele utilizar la siguiente representación alternativa con el bloque derivador o diferenciador

8.9.2. Definiendo el sistema#

Se definen dos sistemas, uno con un cero en el origen y otro con un polo en el origen. También se explicita el rango de frecuencias a utilizar

sistemas = {};
sistemas{1} = zpk([], [0], 1);
sistemas{2} = zpk([0], [], 1);

frecuencia = logspace(-1, 3, 1000);

8.9.3. Magnitud#

La magnitud está definida por:

\[Magnitud(G)=20\cdot \log_{10} (|G(i\omega )|)=20\cdot \log_{10} (|-\frac{1}{\omega }i|)=20\cdot \log_{10} (\frac{|-1|}{|\omega |})=20\cdot \log_{10} (\frac{1}{\omega })=20\cdot \log_{10} (\omega^{-1} )=-20\cdot \log_{10} (\omega )\]

Al utilizar la escala logarítmica la expresión anterior representa una recta que pasa por el punto \((1,0)\) y que tiene una **pendiente negativa }de \(-20dB\)

Cero en el origen

En el caso del cero en el origen se tiene:

\[H(s)=s=\frac{1}{1/s}\]

Por propiedad de los logaritmos se puede expresar como

\[Magnitud(\frac{1}{1/s})=Magnitud(1)-Magnitud(\frac{1}{s})\]

Entonces la magnitud de un cero en el origen puede expresarse como la magnitud de una constante igual a \(1\) menos la magnitud de un polo, entonces:

\[Magnitud(H) = 20\cdot \log_{10} (\omega )\]

Se tiene entonces que la magnitud en frecuencia de un cero en el origen es una recta simétrica con respecto al valor \(0dB\), siendo una recta con una pendiente positiva igual a 20db que pasa por el punto \((1,0)\)

figure; hold all bodemag(sistemas{:}, frecuencia)

legend(“Polo en el origen”, “Cero en el origen”) grid on

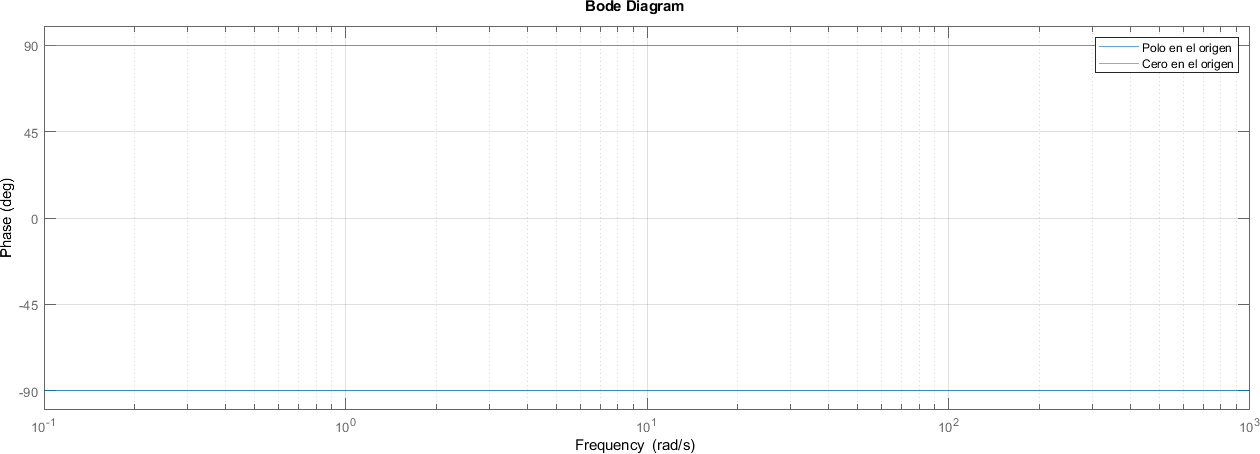
8.9.4. Fase#

Para el cálculo de la fase se tiene

\[\phi =\tan^{-1} \Bigl(\frac{imaginario}{real}\Bigr)=\tan^{-1} \Bigl(-\frac{1/\omega }{0}\Bigr)=-90\]

Por lo tanto la fase será \(-90º\) para todo valor de \(\omega\)

Cero en el origen

Un análisis análogo al de la magnitud puede hacerse para la fase

\[Fase(H) = 90\]

Se concluye entonces que la fase para un sistema con un cero en el origen es de \(90º\)

figure;
hold all

h = bodeplot(sistemas{:}, frecuencia);
setoptions(h, 'MagVisible', 'off');

ylim([-100 100])
legend("Polo en el origen", "Cero en el origen")
grid on
../_images/ELC08_Bode_32_1.png

8.9.5. Interpretación de la simetría entre Cero y Polo en el origen#

La sección anterior mostró como un cero tiene una representación simétrica a un polo, esto puede ilustrarse analíticamente ya que un sistema con un polo y un cero en el origen está definida por

\[W(s)=\frac{s}{s}=1\]

Esto quiere decir que

\[ Magnitud(s)=-Magnitud\left(\frac{1}{s}\right)\]

Análogamente la misma demostración puede aplicarse a la fase quedando

\[Fase(s)=-Fase(\frac{1}{s})\]

8.10. Sistema con un Polo o un Cero Real#

Un sistema con un polo real está definido por

\[G(s)=\frac{1}{s+p}~~p\in {\mathbb{R}}^-\]

Su representación como diagrama de bloques es:

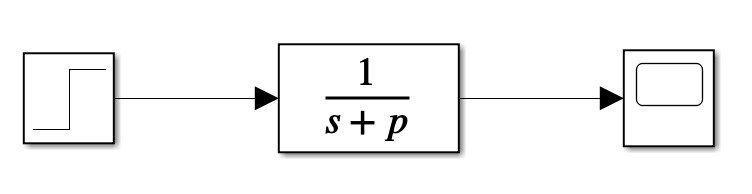
Sin embargo, para facilitar el proceso de graficación se expresará el sistema usando una parametrización alternativa

\[G(s)=\frac{1}{s+p}=\frac{1}{\frac{s}{\omega_0 }+1}~~\omega_o \in {\mathbb{R}}^+\]

En esta parametrización, \(\omega_0\) es la frecuencia de corte.

Luego, utilizando la parametrización de \(G(i\omega )\)se tiene

\[G(i\omega )~=~\frac{1}{\frac{\omega }{\omega_0 }i+1}~=~\frac{1}{\frac{\omega }{\omega_0 }i+1}\cdot \frac{1-\frac{\omega }{\omega_0 }i}{1-\frac{\omega }{\omega_0 }i}~=~\frac{1-\frac{\omega }{\omega_0 }i}{1+\frac{\omega^2 }{\omega_0^2 }}~=~\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}-\frac{\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}i\]

Quedando entonces

\[real=\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}~~~~~imaginario=-\frac{\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}i\]

8.10.1. Definiendo el sistema#

Se definen dos sistemas, uno con una frecuencia de corte de 1 radian y otro con una frecuencia de corte de 10 radianes. También se explicita el rango de frecuencias a utilizar

s = tf("s");

sistemas = {};
sistemas{1} = 1 / (1+s/1);
sistemas{2} = 1 / (1+s/10);

frecuencia = logspace(-1, 3, 1000);

8.10.2. Magnitud#

Utilizando la expresión

\[|G(i\omega )|=\sqrt{real^2 +imaginario^2 }\]

Se tiene entonces

\[|G(i\omega )|=\sqrt{~{\left(\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}~\right)}^2 +~{\left(\frac{-\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}~\right)}^2 }=\sqrt{\frac{1+{\left(\frac{\omega }{\omega_0 }\right)}^2 }{{\left(1+{\left(\frac{\omega }{\omega_0 }\right)}^2 \right)}^2 }}=\sqrt{\frac{1}{1+{\left(\frac{\omega }{\omega_0 }\right)}^2 }}=\sqrt{\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}}={\left(\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}\right)}^{\frac{1}{2}}\]

Una vez en esta forma se puede calcular la magnitud como

\[Magnitud(G)=20\cdot \log_{10} \left({\left(\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}\right)}^{\frac{1}{2}} \right)=10\cdot \log_{10} \left(\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}\right)=-10\cdot \log_{10} \left(1+\frac{\omega^2 }{\omega_0^2 }\right)\]

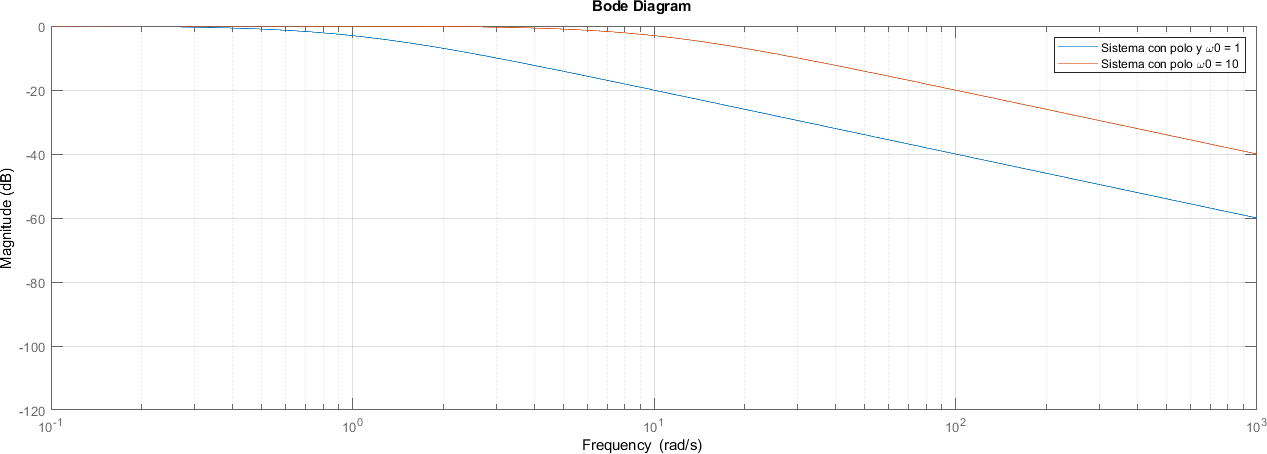
El valor de la magnitud queda entonces definido por una función que puede aproximarse evaluando los puntos críticos de \(\omega\)

\[Magnitud(G)=\left\lbrace \begin{array}{ccccc} -20\log_{10} (\omega /\omega_0 ) & & & ~~\textrm{si} & ~~\omega >>\omega_0 \end{array}\right.\]

Entonces, la función aproximada puede representarse de la siguiente manera: cuando \(\omega\) es mucho menor que la frecuencia de corte entonces la magnitud es nula, a medida que \(\omega\) se acerca a la frecuencia de corte, la magnitud baja hasta llegar a \(-3dB\) y a partir de ese momento sigue una línea recta con una pendiente negativa de \(20dB\), esa recta es la que pasa por el punto \((\omega_0 ,0)\)

La magnitud para un polo real tiene tres puntos críticos, el primero es el valor inicial que será

figure;
hold all

bodemag(sistemas{:}, frecuencia)

legend("Sistema con polo y \omega0 = 1", "Sistema con polo \omega0 = 10")
ylim([-120 0])
grid on
../_images/ELC08_Bode_40_1.png

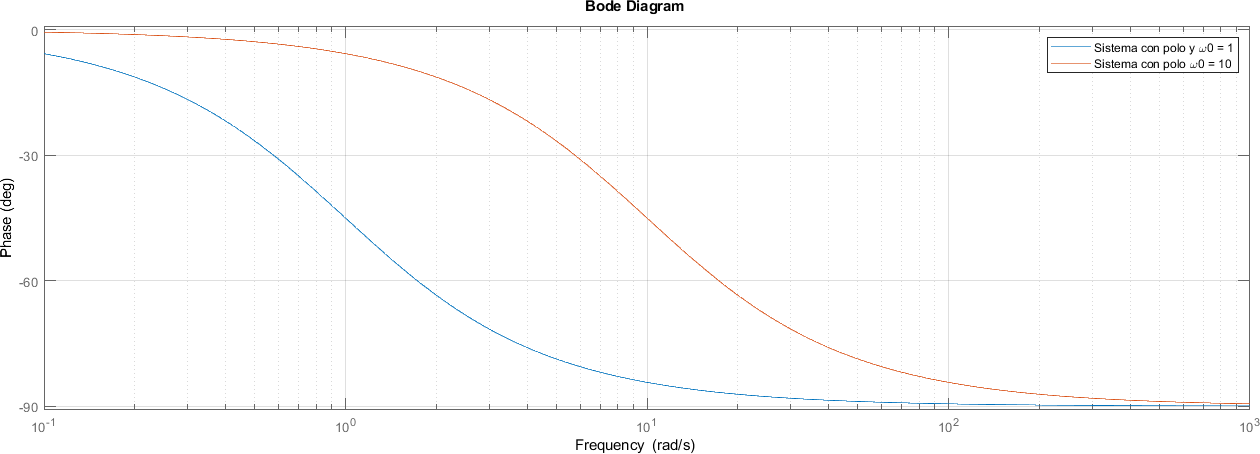
8.10.3. Fase#

Utilizando la expresión

\[Fase(G)=~\phi =\tan^{-1} \Bigl(\frac{imaginario}{real}\Bigr)\]

Se tiene que la fase es

\[Fase(G)~=~\phi ~=~\tan^{-1} \left(\frac{\left(\frac{-\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}\right)}{\left(\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}\right)}\right)~=~\tan^{-1} \left(\frac{-\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}\cdot \frac{1}{\frac{1}{1+\frac{\omega^2 }{\omega_0^2 }}}\right)~=~\tan^{-1} \left(\frac{-\frac{\omega }{\omega_0 }}{1+\frac{\omega^2 }{\omega_0^2 }}\cdot \left(1+\frac{\omega^2 }{\omega_0^2 }\right)\right)~=~\tan^{-1} \left(-\frac{\omega }{\omega_0 }\right)\]

Nuevamente, la Fase entonces puede aproximarse viendo los valores críticos de \(\omega\)

\[Fase(G)=\left\lbrace \begin{array}{ccccc} \tan^{-1} (-\infty ) & = & -\pi /2 & ~~\textrm{si} & ~~\omega >>\omega_0 \end{array}\right.\]

De esta forma, cuando el valor de \(\omega\) es mucho menor a la frecuencia de corte la fase de 0º, a medida que \(\omega\) se acerca a la frecuencia de corte el valor se acerca a \(-45º\) ( \(-\pi /4\) radiantes) y cuando \(\omega\) es mucho mayor que la frecuencia de corte, la fase se acerca asintóticamente a \(-90º\) ( \(-\pi /2\) radianes)

figure;
hold all

h = bodeplot(sistemas{:}, frecuencia);
setoptions(h, 'MagVisible', 'off');

legend("Sistema con polo y \omega0 = 1", "Sistema con polo \omega0 = 10")
grid on
../_images/ELC08_Bode_46_1.png

8.10.4. Cero Real#

En el caso de un cero real, un análisis similar al de la simetría visto en la sección anterior pueden hacerse en este caso.

Si \(H(s)\)es una función con un cero real

\[H(s)=s+z=\frac{1}{1/(s+z)}\]

Se tiene que

\[W(s)=\frac{s+z}{s+z}=1\]

Entonces

\[Magnitud\left(s+z\right)=-Magnitud\left(\frac{1}{s+z}\right)\]

Análogamente la misma demostración puede aplicarse a la fase quedando

\[Fase\left(s+z\right)=-Fase\left(\frac{1}{s+z}\right)\]

Se concluye entonces que un sistema con un cero real tiene una representación en el dominio de la frecuencia simétrica a la de un sistema con un polo real.

8.10.5. Definiendo el sistema#

Se definen dos sistemas con la misma frecuencia de corte que los anteriores pero con ceros en vez polos. También se explicita el rango de frecuencias a utilizar

sistemas{3} = (1+s/1);
sistemas{4} = (1+s/10);

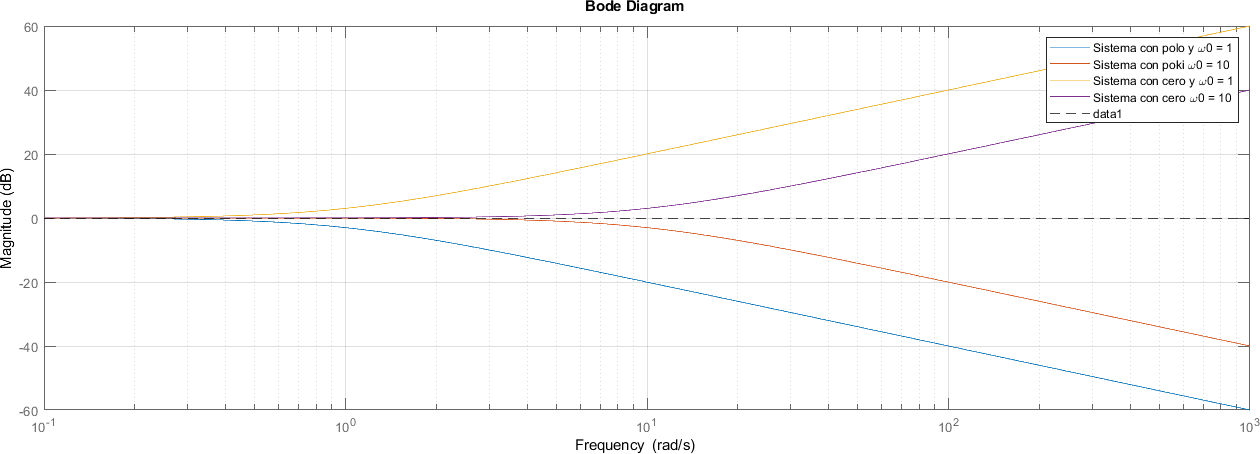
8.10.6. Magnitud#

figure;
hold all

bodemag(sistemas{:}, frecuencia)

legend("Sistema con polo y \omega0 = 1", "Sistema con poki \omega0 = 10", "Sistema con cero y \omega0 = 1", "Sistema con cero \omega0 = 10")
ylim([-60 60])
yline(0, "--k")
grid on
../_images/ELC08_Bode_51_1.png

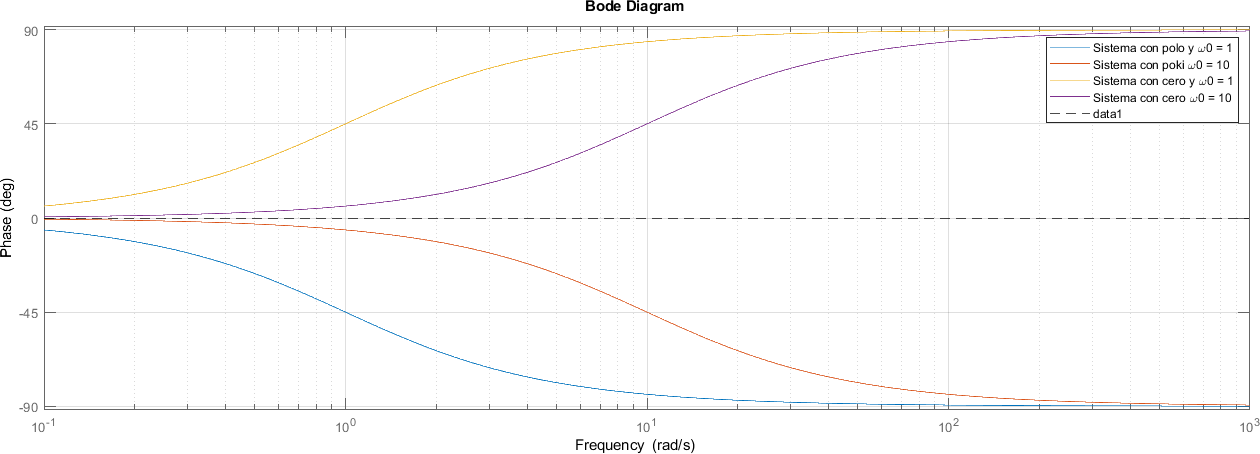
8.10.7. Fase#

figure;
hold all

h = bodeplot(sistemas{:}, frecuencia);
setoptions(h, 'MagVisible', 'off');

legend("Sistema con polo y \omega0 = 1", "Sistema con poki \omega0 = 10", "Sistema con cero y \omega0 = 1", "Sistema con cero \omega0 = 10")
yline(0, "--k")
grid on
../_images/ELC08_Bode_53_1.png

8.11. Sistema con un Polo o un Cero Complejo#

sistemas = {};
sistemas{1} = 1;
sistemas{2} = 1;
sistemas{3} = 1;

8.11.1. Magnitud#

%TODO

8.11.2. Fase#

%TODO

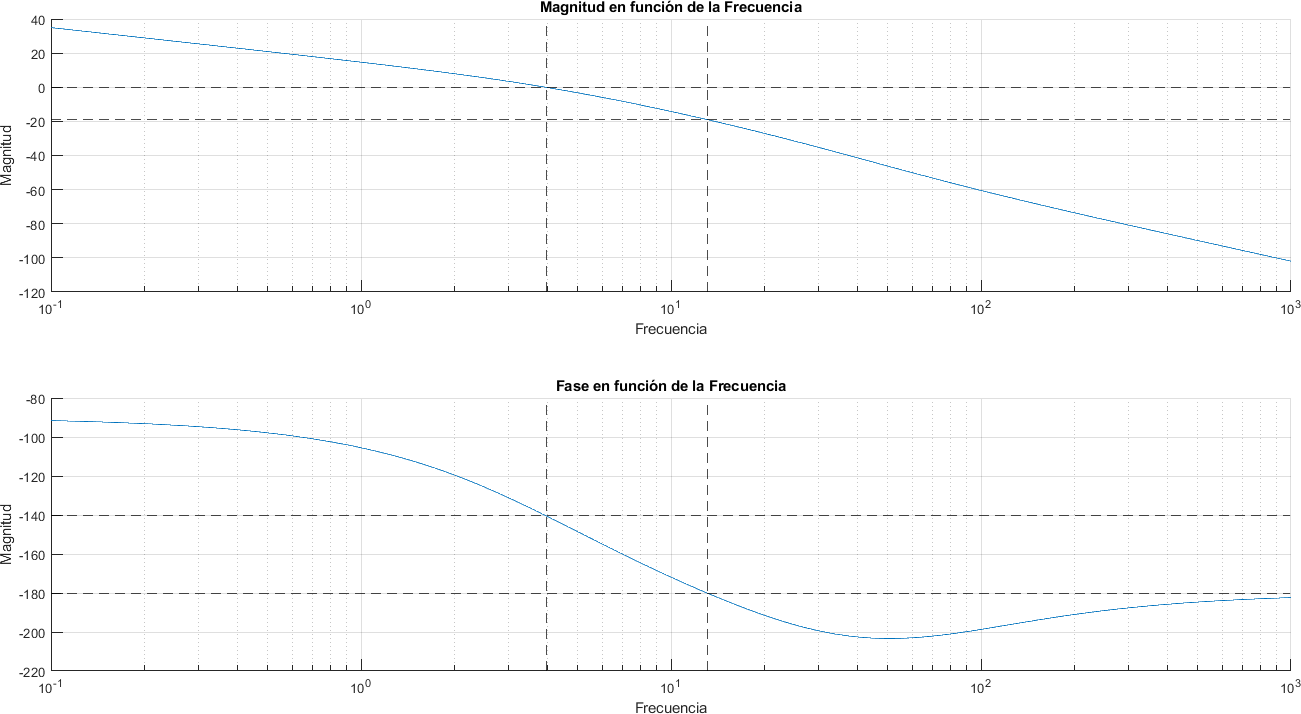
8.12. Evaluando Estabilidad#

Se puede evaluar estabilidad si para un desfase de 180 la amplitud de la salida es menor que 1. Como se utiliza la escala logarítmica esto equivale a decir que es menor a 0 dB

%plot inline --format=png -w 1600 -h 800

sistema = zpk([-70], [0 -4 -25], 8);

frecuencia = logspace(-1, 3, 1000);
[magnitud, fase, frecuencia] = bode(sistema, frecuencia);
magnitud = 20 * log10(magnitud);

[minimo, magnitud_indice_minimo] = min(abs(magnitud));
frecuencia_cruce_ganancia = frecuencia(magnitud_indice_minimo);

[minimo, fase_indice_minimo] = min(abs(fase+180));
frecuencia_cruce_fase = frecuencia(fase_indice_minimo);

margen_ganancia = 1 / -magnitud(fase_indice_minimo);
margen_fase = 180 + fase(magnitud_indice_minimo);

figure;
ax = subplot(2, 1, 1);
hold(ax, "on");
plot(frecuencia, reshape(magnitud, [1, length(frecuencia)]))
yline(0, "--k")
yline(magnitud(fase_indice_minimo), "--k")
xline(frecuencia_cruce_ganancia, "--k")
xline(frecuencia_cruce_fase, "--k")
set(gca, 'XScale', 'log')
xlabel("Frecuencia")
ylabel("Magnitud")
title("Magnitud en función de la Frecuencia")
grid("on")

ax = subplot(2, 1, 2);
hold(ax, "on");
plot(frecuencia, reshape(fase, [1, length(frecuencia)]))
xline(frecuencia_cruce_ganancia, "--k")
xline(frecuencia_cruce_fase, "--k")
yline(-180, "--k")
yline(fase(magnitud_indice_minimo), "--k")
set(gca, 'XScale', 'log')
xlabel("Frecuencia")
ylabel("Magnitud")
title("Fase en función de la Frecuencia")
grid("on")
../_images/ELC08_Bode_62_1.png

8.13. Criterio de Estabilidad#

Un sistema es estable si cualquiera de las siguientes condiciones equivalentes se cumplen

  1. El margen de ganancia y el margen de fase son ambos mayores a cero

margen_ganancia, margen_fase

margen_ganancia =
    0.0526
margen_fase =
   39.5326

Calculando \(K_p\) dado un margen de ganancia

%TODO

  1. La frecuencia de Cruce de Ganancia es menor que la frecuencia de Cruce de Fase

frecuencia_cruce_ganancia, frecuencia_cruce_fase

frecuencia_cruce_ganancia =
    3.9591
frecuencia_cruce_fase =
   13.1256

  1. Si la amplitud asociada a la frecuencia de Cruce de Fase (desfase de -180) es menor a 1 o análogamente menor a 0 dB

magnitud(fase_indice_minimo)

ans =
  -19.0127

8.14. Forma automática de calcular márgenes#

allmargin(sistema)

ans = 
  struct with fields:

     GainMargin: [8.8444 Inf]
    GMFrequency: [13.0685 Inf]
    PhaseMargin: 39.6681
    PMFrequency: 3.9435
    DelayMargin: 0.1756
    DMFrequency: 3.9435
         Stable: 1

figure;
margin(sistema)
grid on
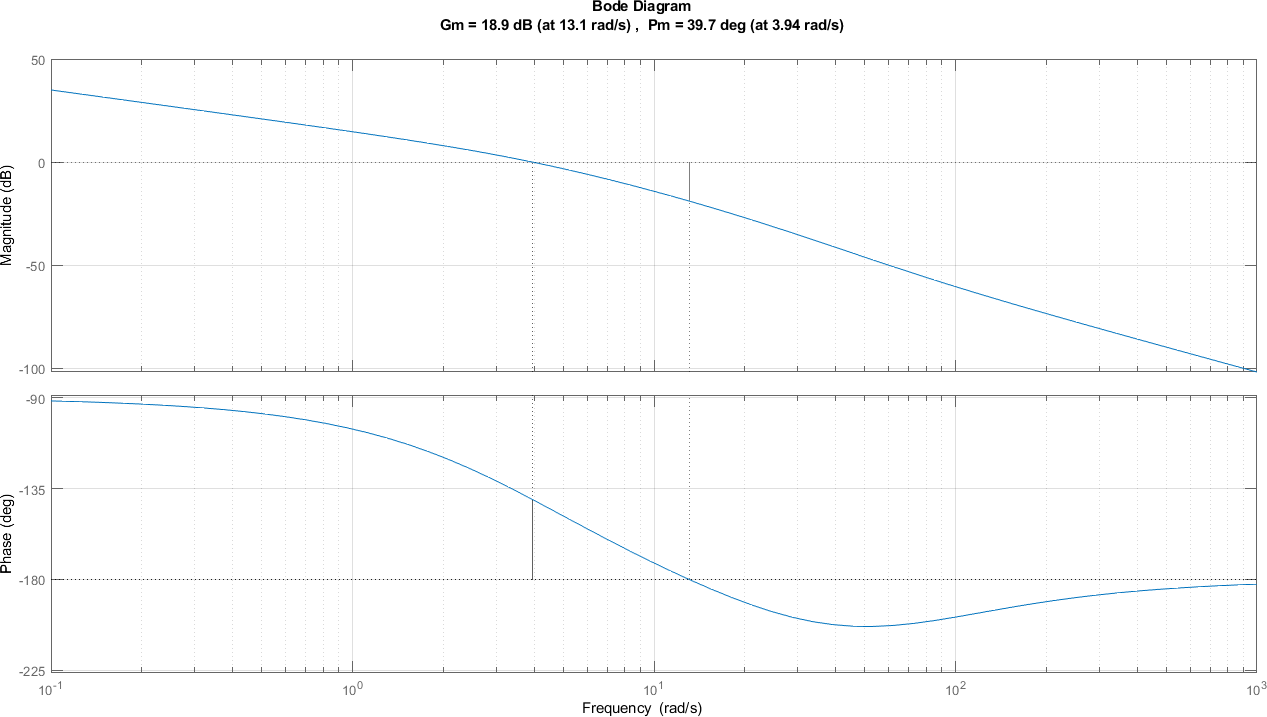
../_images/ELC08_Bode_73_1.png

8.15. Casos#

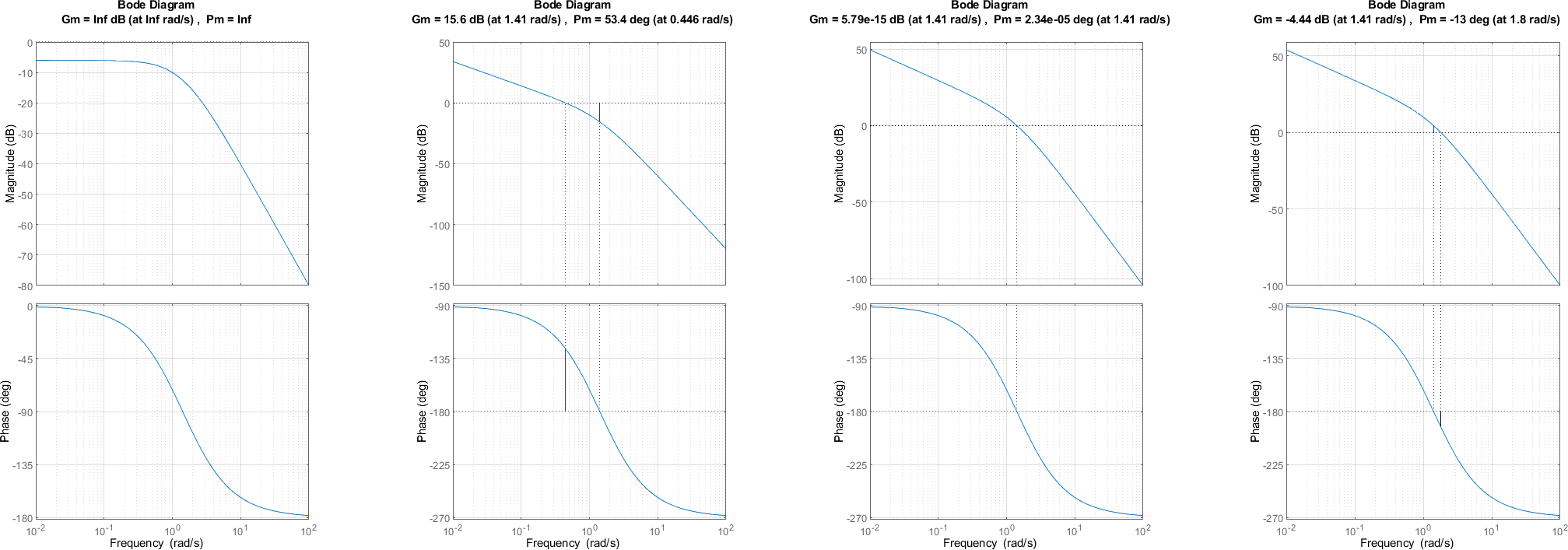
Existen 4 casos al evaluar sistemas de fase mínima con los diagramas de Bode

  1. El sistema tiene un margen de ganancia infinito: la magnitud se encuentra por debajo de la línea de los 0dB y se corresponde con sistemas que son estables para cualquier valor de \(K\)

  2. El sistema tiene un margen de ganancia finito y positivo: la magnitud para la frecuencia de cruce de fase es negativa y se corresponde con un sistema que es estable para el valor actual de \(K\) pero no no será estable si se aumenta el \(K\)más allá del valor crítico.

  3. El sistema tiene un margen de ganancia nulo: la magnitud es nula para la frecuencia de cruce de fase y se corresponde con un sistema críticamente estable.

  4. El sistema tiene un margen de ganancia finito y negativo: la magnitud para la frecuencia de cruce de fase es positiva y se corresponde con un sistema que es inestable para el valor actual de \(k\)** pero que será estable si se aumenta el \(K\) más allá del valor crítico.

No existe la posibilidad que el sistema sea inestable para todo \(K\) con un diagrama de Bode ya que esos sistemas no son de fase mínima.

%plot inline --format=png -w 2600 -h 800

figure;

subplot(1, 4, 1)
[num, den] = zp2tf([], [-1 -2], 1);
sistema = tf(num, den);
margin(sistema)
grid on

subplot(1, 4, 2)
sistema = tf([1], [1 3 2 0]);
margin(sistema)
grid on

subplot(1, 4, 3)
sistema = tf([1], [1 3 2 0]);
margin(6*sistema)
grid on

subplot(1, 4, 4)
sistema = tf([1], [1 3 2 0]);
margin(10*sistema)
grid on
../_images/ELC08_Bode_76_1.png

8.16. Ancho de banda#

%plot inline --format=png -w 1600 -h 500

sistema = zpk([-70], [0 -4 -25], 8);

lazo_cerrado = feedback(sistema, 1);

frecuencia = logspace(-1, 2, 1000);
[magnitud, fase, frecuencia] = bode(lazo_cerrado, frecuencia);
magnitud = 20 * log10(magnitud);

[pico_de_resonancia, magnitud_indice_maximo] = max(magnitud);
frecuencia_pico_de_resonancia = frecuencia(magnitud_indice_maximo);

[magitud_ancho_de_banda, magitud_indice_ancho] = min(abs(magnitud+3));
ancho_de_banda = frecuencia(magitud_indice_ancho);


figure('Position', [0 0 1600 400]);
hold on
plot(frecuencia, reshape(magnitud, [1, length(frecuencia)]))

yline(-3, "--k")
yline(pico_de_resonancia, "--k")
xline(frecuencia_pico_de_resonancia, "--k")
xline(ancho_de_banda, "--k")

set(gca, 'XScale', 'log')
xlabel("Frecuencia")
ylabel("Magnitud")
title("Pico de Resonancia")
grid("on")
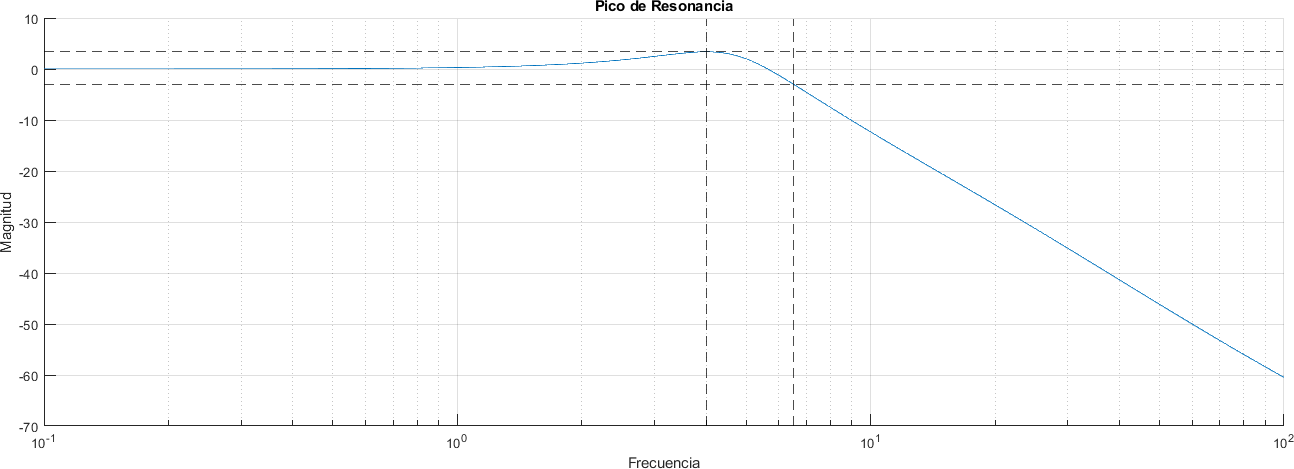
../_images/ELC08_Bode_79_1.png

A mayor pico de resonancia, mayor overshoot

pico_de_resonancia

pico_de_resonancia =
    3.3750

A mayor ancho de banda, mayor velocidad de respuesta

ancho_de_banda

ancho_de_banda =
    6.5135

8.17. Casos#

Existen 3 posibles casos para los sistemas

  1. Subamortiguado

  2. Sobrearmotiguado

  3. Críticamente amortiguado

Los subamortiguados tendrán un pico de resonancia positivo y será proporcional al coeficiente relativo de amortiguamiento. En el caso de los críticamente amortiguados y los sobreamortiguados, tendrán pico de resonancia menor o incluso inexistente, dependiendo del valor de \(\zeta\).

Por otro lado, el ancho de banda está directamente relacionado con la velocidad de respuesta del sistema

s = tf("s");
Kp = 1;
Ki = 1;
controlador = Kp + Ki / s;

subamortiguado = controlador * zpk([], [-1+3j -1-3j], 15);
subamortiguado_lazo_cerrado = feedback(subamortiguado, 1);

criticamente_amortiguado = controlador * zpk([], [-1 -1], 0.25);
criticamente_amortiguado_lazo_cerrado = feedback(criticamente_amortiguado, 1);

sobreamortiguado = controlador * zpk([], [-1.5 -0.5], 0.1);
sobreamortiguado_lazo_cerrado = feedback(sobreamortiguado, 1);

Diagrama de Bode

%plot inline --format=png -w 2200 -h 500

figure;

subplot(1, 2, 1)
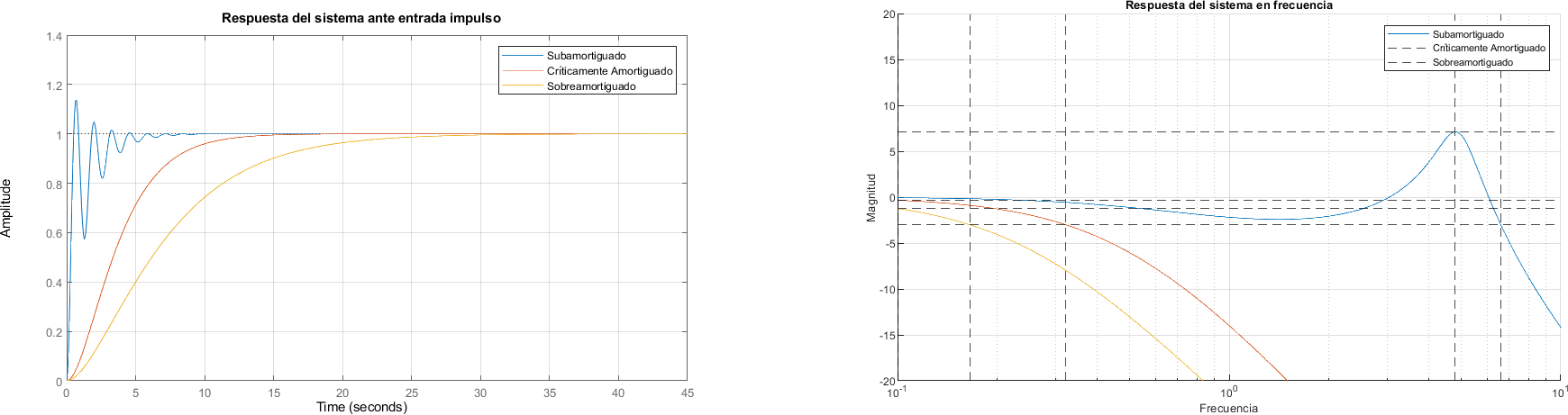
step(subamortiguado_lazo_cerrado, criticamente_amortiguado_lazo_cerrado, sobreamortiguado_lazo_cerrado)
legend("Subamortiguado", "Críticamente Amortiguado", "Sobreamortiguado")
title("Respuesta del sistema ante entrada impulso")
ylim([0 1.4])
grid on

ax = subplot(1, 2, 2);
hold(ax, "on")
frecuencia = logspace(-1, 1, 1000);
for lazo_cerrado = [subamortiguado_lazo_cerrado, criticamente_amortiguado_lazo_cerrado, sobreamortiguado_lazo_cerrado]
    [magnitud, fase, frecuencia] = bode(lazo_cerrado, frecuencia);
    magnitud = 20 * log10(magnitud);
    
    [pico_de_resonancia, magnitud_indice_maximo] = max(magnitud);
    frecuencia_pico_de_resonancia = frecuencia(magnitud_indice_maximo);
    
    [magitud_ancho_de_banda, magitud_indice_ancho] = min(abs(magnitud+3));
    ancho_de_banda = frecuencia(magitud_indice_ancho);
    
    plot(frecuencia, reshape(magnitud, [1, length(frecuencia)]))
    
    yline(pico_de_resonancia, "--k")
    xline(frecuencia_pico_de_resonancia, "--k")
    xline(ancho_de_banda, "--k")
    set(gca, 'XScale', 'log')

end

set(gca, 'XScale', 'log')
xlabel("Frecuencia")
ylabel("Magnitud")
yline(-3, "--k")
ylim([-20 20])
legend("Subamortiguado", "Críticamente Amortiguado", "Sobreamortiguado")
title("Respuesta del sistema en frecuencia")
grid("on")
../_images/ELC08_Bode_88_1.png